Chapter 3 Path Analysis
3.1 Syntax - R
library(lavaan); library(semPlot)3.1.1 Use a sample covariance matrix an input
COV <- '
160
106 210
129 109 225 '
typeof(COV)## [1] "character"class(COV)## [1] "character"mr.cov <- getCov(COV, names = c("Y", "X1", "X2")) #create full covariance matrix
mr.cov## Y X1 X2
## Y 160 106 129
## X1 106 210 109
## X2 129 109 225typeof(mr.cov)## [1] "double"class(mr.cov)## [1] "matrix" "array"3.1.1.1 Specify and fit the regression model
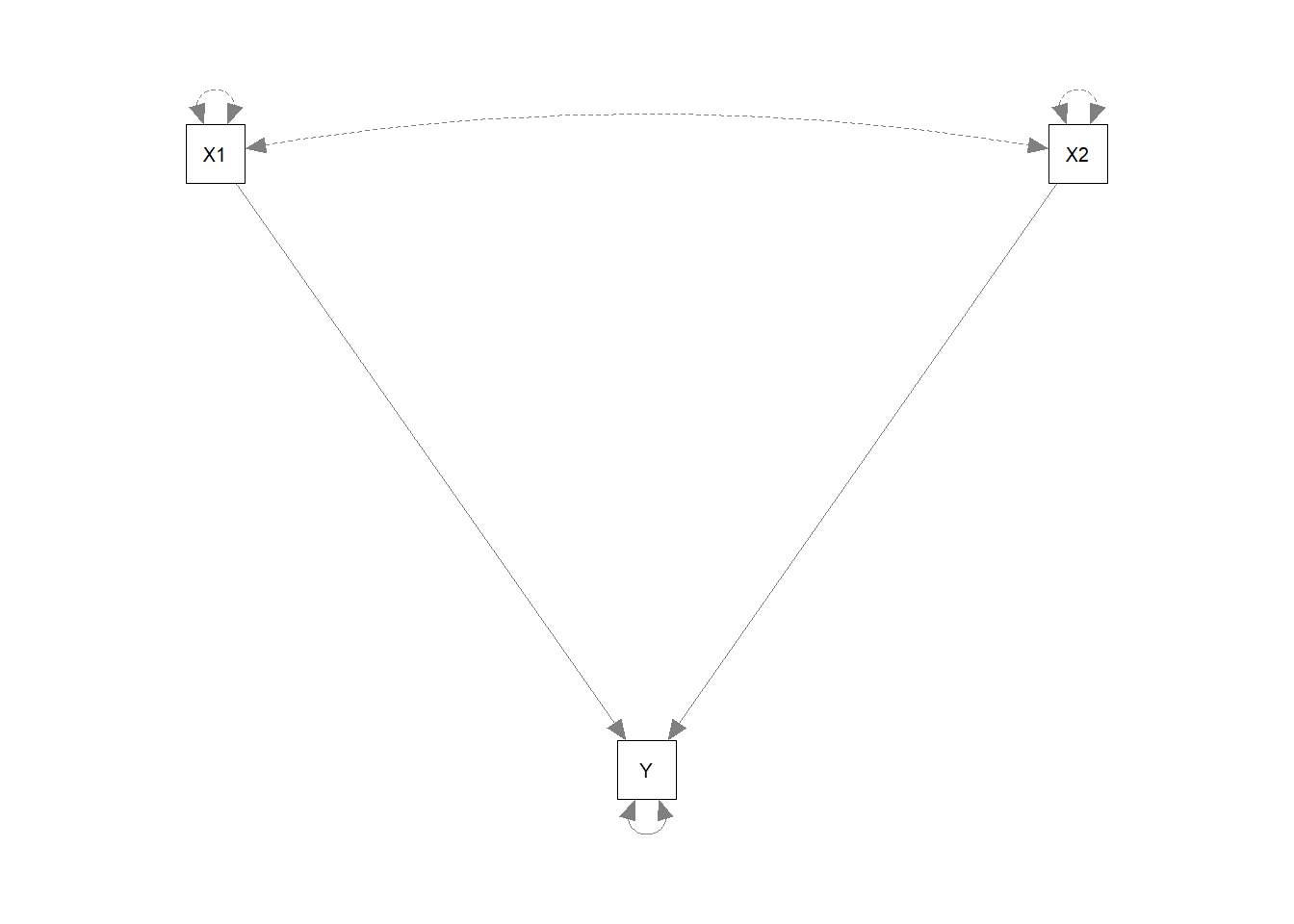
mr.model <- ' Y ~ X1 + X2 '
mr.fit1 <- sem(mr.model, sample.cov = mr.cov, sample.nobs = 256)
summary(mr.fit1, fit.measures = TRUE, standardized = TRUE)## lavaan 0.6-8 ended normally after 11 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 3
##
## Number of observations 256
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Model Test Baseline Model:
##
## Test statistic 197.408
## Degrees of freedom 2
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 1.000
## Tucker-Lewis Index (TLI) 1.000
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -913.665
## Loglikelihood unrestricted model (H1) -913.665
##
## Akaike (AIC) 1833.331
## Bayesian (BIC) 1843.966
## Sample-size adjusted Bayesian (BIC) 1834.456
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.000
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.000
## P-value RMSEA <= 0.05 NA
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.000
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Y ~
## X1 0.277 0.043 6.454 0.000 0.277 0.317
## X2 0.439 0.041 10.603 0.000 0.439 0.521
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Y 73.710 6.515 11.314 0.000 73.710 0.4623.1.1.2 Mimic mplus results
mr.fit2 <- sem(mr.model, sample.cov = mr.cov, sample.nobs = 256, mimic = "Mplus")
summary(mr.fit2, fit.measures = TRUE, standardized = TRUE)## lavaan 0.6-8 ended normally after 11 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 4
##
## Number of observations 256
##
## Model Test User Model:
##
## Test statistic 0.000
## Degrees of freedom 0
##
## Model Test Baseline Model:
##
## Test statistic 197.408
## Degrees of freedom 2
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 1.000
## Tucker-Lewis Index (TLI) 1.000
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -913.665
## Loglikelihood unrestricted model (H1) -913.665
##
## Akaike (AIC) 1835.331
## Bayesian (BIC) 1849.512
## Sample-size adjusted Bayesian (BIC) 1836.831
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.000
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.000
## P-value RMSEA <= 0.05 NA
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.000
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Observed
## Observed information based on Hessian
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Y ~
## X1 0.277 0.043 6.454 0.000 0.277 0.317
## X2 0.439 0.041 10.603 0.000 0.439 0.521
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Y 0.000 0.537 0.000 1.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Y 73.710 6.515 11.314 0.000 73.710 0.4623.1.2 Use sample correlation matrix and SDs as input
CORR <- '
1.000
.498 1.000
.738 .643 1.000
.649 .721 .823 1.000'
SDs <- c(13.76, 10.41, 15.00, 13.29)
pa.cov <- getCov(CORR)
pa.cov <- cor2cov(pa.cov, sds = SDs, names = c("X", "Y1", "Y2", "Y3"))pa.model <- '
Y1 ~ b*Y2
Y2 ~ a*X
Y3 ~ c*Y1 + d*Y2
#indirect effects
ad :=a*d
abc :=a*b*c
bc :=b*c
#total effects
XtoY3 := ad+abc
Y2toY3 :=d+bc'
pa.fit <- sem(pa.model, sample.cov=pa.cov, sample.nobs = 116, mimic = "Mplus")
# pa.fit2 <- sem(pa.model, sample.cov=pa.cov, sample.nobs = 116)
# When mimic="Mplus", the number of free parameters is NOT consistent with Mplus output for this example. However, that is NOT always the case.
summary(pa.fit, fit.measures = TRUE, standardized = TRUE)## lavaan 0.6-8 ended normally after 15 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 10
##
## Number of observations 116
##
## Model Test User Model:
##
## Test statistic 1.377
## Degrees of freedom 2
## P-value (Chi-square) 0.502
##
## Model Test Baseline Model:
##
## Test statistic 310.802
## Degrees of freedom 6
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 1.000
## Tucker-Lewis Index (TLI) 1.006
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -1223.560
## Loglikelihood unrestricted model (H1) -1222.871
##
## Akaike (AIC) 2467.120
## Bayesian (BIC) 2494.656
## Sample-size adjusted Bayesian (BIC) 2463.046
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.000
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.165
## P-value RMSEA <= 0.05 0.594
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.013
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Observed
## Observed information based on Hessian
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Y1 ~
## Y2 (b) 0.446 0.049 9.042 0.000 0.446 0.643
## Y2 ~
## X (a) 0.805 0.068 11.779 0.000 0.805 0.738
## Y3 ~
## Y1 (c) 0.417 0.079 5.291 0.000 0.417 0.327
## Y2 (d) 0.543 0.055 9.913 0.000 0.543 0.613
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Y1 0.000 0.737 0.000 1.000 0.000 0.000
## .Y2 0.000 0.936 0.000 1.000 0.000 0.000
## .Y3 0.000 0.626 0.000 1.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Y1 63.015 8.274 7.616 0.000 63.015 0.587
## .Y2 101.572 13.337 7.616 0.000 101.572 0.455
## .Y3 45.517 5.977 7.616 0.000 45.517 0.260
##
## Defined Parameters:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## ad 0.437 0.058 7.585 0.000 0.437 0.452
## abc 0.150 0.035 4.258 0.000 0.150 0.155
## bc 0.186 0.041 4.566 0.000 0.186 0.210
## XtoY3 0.587 0.062 9.401 0.000 0.587 0.607
## Y2toY3 0.729 0.047 15.604 0.000 0.729 0.823#obtain model-implied (fitted) covariance matrix and mean vector
fitted(pa.fit)## $cov
## Y1 Y2 Y3 X
## Y1 107.434
## Y2 99.539 223.060
## Y3 98.890 162.651 175.101
## X 67.387 151.010 110.113 187.705
##
## $mean
## Y1 Y2 Y3 X
## 0 0 0 0#obtain unstandardized residuals of a fitted model
resid(pa.fit)## $type
## [1] "raw"
##
## $cov
## Y1 Y2 Y3 X
## Y1 0.000
## Y2 0.000 0.000
## Y3 0.000 0.000 0.000
## X 3.332 0.000 7.547 0.000
##
## $mean
## Y1 Y2 Y3 X
## 0 0 0 0#obtain standardized residuals of a fitted model
resid(pa.fit, type="standardized")## $type
## [1] "standardized"
##
## $cov
## Y1 Y2 Y3 X
## Y1 0.000
## Y2 0.000 0.000
## Y3 0.000 0.000 0.000
## X 0.470 0.000 1.013 0.000
##
## $mean
## Y1 Y2 Y3 X
## 0 0 0 0#obtain the estimated covariance matrix of parameter estimates
vcov(pa.fit) ## b a c d Y1~~Y1 Y2~~Y2 Y3~~Y3 Y1~1 Y2~1
## b 0.002
## a 0.000 0.005
## c 0.000 0.000 0.006
## d 0.000 0.000 -0.003 0.003
## Y1~~Y1 0.000 0.000 0.000 0.000 68.465
## Y2~~Y2 0.000 0.000 0.000 0.000 0.000 177.877
## Y3~~Y3 0.000 0.000 0.000 0.000 0.000 0.000 35.721
## Y1~1 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.543
## Y2~1 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.876
## Y3~1 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
## Y3~1
## b
## a
## c
## d
## Y1~~Y1
## Y2~~Y2
## Y3~~Y3
## Y1~1
## Y2~1
## Y3~1 0.3923.1.3 Path analysis model - Wheaton et al. (1977) example
lower <- '12.892,
7.064, 9.237,
7.417, 5.205, 12.585
5.077, 5.091, 7.375, 10.036'
wheaton.cov <- getCov(lower, names = c("anomia67","powerless67", "anomia71", "powerless71"))
wheaton.model <- '
anomia71 ~ anomia67 + powerless67
powerless71 ~ anomia67 + powerless67
anomia67 ~~ powerless67
anomia71 ~~ 0*powerless71'
wheaton.fit <- sem(wheaton.model, sample.cov = wheaton.cov, sample.nobs = 932, mimic = "Mplus")
# wheaton.fit2 <- sem(wheaton.model, sample.cov = wheaton.cov, sample.nobs = 932)
summary(wheaton.fit, fit.measures = TRUE, standardized = TRUE)## lavaan 0.6-8 ended normally after 26 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 13
##
## Number of observations 932
##
## Model Test User Model:
##
## Test statistic 301.214
## Degrees of freedom 1
## P-value (Chi-square) 0.000
##
## Model Test Baseline Model:
##
## Test statistic 1550.935
## Degrees of freedom 6
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.806
## Tucker-Lewis Index (TLI) -0.166
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -9145.166
## Loglikelihood unrestricted model (H1) -8994.559
##
## Akaike (AIC) 18316.331
## Bayesian (BIC) 18379.217
## Sample-size adjusted Bayesian (BIC) 18337.930
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.568
## 90 Percent confidence interval - lower 0.515
## 90 Percent confidence interval - upper 0.622
## P-value RMSEA <= 0.05 0.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.094
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Observed
## Observed information based on Hessian
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## anomia71 ~
## anomia67 0.459 0.034 13.490 0.000 0.459 0.464
## powerless67 0.213 0.040 5.291 0.000 0.213 0.182
## powerless71 ~
## anomia67 0.158 0.032 4.975 0.000 0.158 0.179
## powerless67 0.430 0.038 11.467 0.000 0.430 0.413
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## anomia67 ~~
## powerless67 7.056 0.425 16.590 0.000 7.056 0.647
## .anomia71 ~~
## .powerless71 0.000 0.000 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .anomia71 0.000 0.093 0.000 1.000 0.000 0.000
## .powerless71 0.000 0.087 0.000 1.000 0.000 0.000
## anomia67 0.000 0.118 0.000 1.000 0.000 0.000
## powerless67 0.000 0.100 0.000 1.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .anomia71 8.067 0.374 21.587 0.000 8.067 0.642
## .powerless71 7.035 0.326 21.587 0.000 7.035 0.702
## anomia67 12.878 0.597 21.587 0.000 12.878 1.000
## powerless67 9.227 0.427 21.587 0.000 9.227 1.000semPlot::semPaths(wheaton.fit)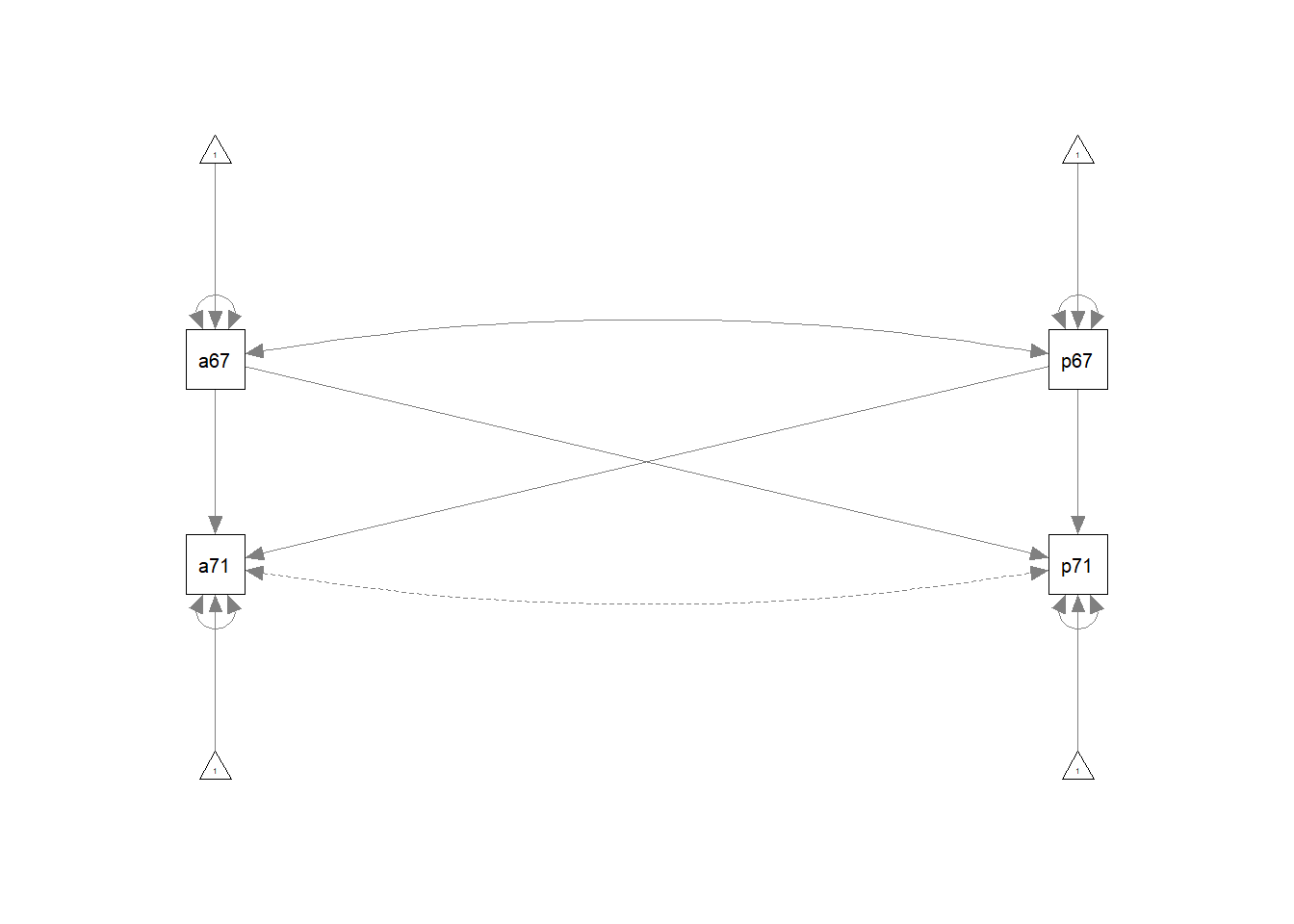
3.1.4 Use raw data as input
rawdat <- read.fwf("data/wheaton-generated.dat", widths=rep(8,6),header = FALSE, col.names = c("anomia67", "powerless67", "anomia71", "powerless71", "educ", "sei"))
head(rawdat)## anomia67 powerless67 anomia71 powerless71 educ sei
## 1 3.68 4.30 5.30 2.84 4.74 24.88
## 2 3.14 -0.17 1.43 4.82 5.52 23.70
## 3 10.77 6.31 7.14 5.02 0.70 19.82
## 4 8.90 6.30 9.39 6.58 0.33 18.31
## 5 13.12 9.71 11.97 10.48 -0.27 16.96
## 6 3.06 4.57 4.45 6.68 0.73 20.94Alternatively, you can import the original SPSS dataset use the import function from the rio package.
Pay attention to the variable names. R is case sensitive. SPSS, like Mplus, is case insensitive.
library(rio)
rawdat2 <- import("data/wheaton-generated.sav")
head(rawdat2)Fit the model using the sem() function from lavaan.
wheaton.model <- '
anomia71 ~ anomia67 + powerless67
powerless71 ~ anomia67 + powerless67
anomia67 ~~ powerless67
anomia71 ~~ 0*powerless71'
wheaton.fit.rawdat <- sem(wheaton.model, data=rawdat, mimic = "Mplus")
summary(wheaton.fit.rawdat, fit.measures = TRUE, standardized = TRUE)
wheaton.fit2.rawdat <- sem(wheaton.model, data=rawdat)
summary(wheaton.fit2.rawdat, fit.measures = TRUE, standardized = TRUE)3.2 Syntax - Mplus
3.2.1 Regression of Y on X1 and X2 - sample covariance matrix
TITLE: Multiple regression with two independent variables
DATA: FILE IS "data\COV.DAT";
TYPE IS COVARIANCE;
NOBSERVATIONS ARE 256;
VARIABLE: NAMES ARE Y X1 X2;
MODEL: Y ON X1 X2;
X1 WITH X2;
OUTPUT: SAMPSTAT STANDARDIZED RESIDUAL CINTERVAL;## Mplus VERSION 8.4
## MUTHEN & MUTHEN
## 06/10/2021 12:19 PM
##
## INPUT INSTRUCTIONS
##
## TITLE: Multiple regression with two independent variables
## DATA: FILE IS "data\COV.DAT";
## TYPE IS COVARIANCE;
## NOBSERVATIONS ARE 256;
## VARIABLE: NAMES ARE Y X1 X2;
## MODEL: Y ON X1 X2;
## X1 WITH X2;
## OUTPUT: SAMPSTAT STANDARDIZED RESIDUAL CINTERVAL;
##
##
##
## 1 ERROR(S) FOUND IN THE INPUT INSTRUCTIONS
##
##
##
## Multiple regression with two independent variables
##
## SUMMARY OF ANALYSIS
##
## Number of groups 1
## Number of observations 256
##
## Number of dependent variables 1
## Number of independent variables 2
## Number of continuous latent variables 0
##
## Observed dependent variables
##
## Continuous
## Y
##
## Observed independent variables
## X1 X2
##
##
## Estimator ML
## Information matrix EXPECTED
## Maximum number of iterations 1000
## Convergence criterion 0.500D-04
## Maximum number of steepest descent iterations 20
##
## Input data file(s)
## data\COV.DAT
##
## Input data format FREE
##
##
## SAMPLE STATISTICS
##
##
## SAMPLE STATISTICS
##
##
## Covariances/Correlations/Residual Correlations
## Y X1 X2
## ________ ________ ________
## Y 160.000
## X1 106.000 210.000
## X2 129.000 109.000 225.000
##
##
## THE MODEL ESTIMATION TERMINATED NORMALLY
##
##
##
## MODEL FIT INFORMATION
##
## Number of Free Parameters 6
##
## Loglikelihood
##
## H0 Value -2979.780
## H1 Value -2979.780
##
## Information Criteria
##
## Akaike (AIC) 5971.559
## Bayesian (BIC) 5992.830
## Sample-Size Adjusted BIC 5973.809
## (n* = (n + 2) / 24)
##
## Chi-Square Test of Model Fit
##
## Value 0.000
## Degrees of Freedom 0
## P-Value 0.0000
##
## RMSEA (Root Mean Square Error Of Approximation)
##
## Estimate 0.000
## 90 Percent C.I. 0.000 0.000
## Probability RMSEA <= .05 0.000
##
## CFI/TLI
##
## CFI 1.000
## TLI 1.000
##
## Chi-Square Test of Model Fit for the Baseline Model
##
## Value 197.408
## Degrees of Freedom 2
## P-Value 0.0000
##
## SRMR (Standardized Root Mean Square Residual)
##
## Value 0.000
##
##
##
## MODEL RESULTS
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Y ON
## X1 0.277 0.043 6.454 0.000
## X2 0.439 0.041 10.603 0.000
##
## X1 WITH
## X2 108.576 15.139 7.172 0.000
##
## Variances
## X1 209.182 18.489 11.314 0.000
## X2 224.125 19.810 11.314 0.000
##
## Residual Variances
## Y 73.716 6.516 11.314 0.000
##
##
## STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Y ON
## X1 0.317 0.048 6.595 0.000
## X2 0.521 0.045 11.638 0.000
##
## X1 WITH
## X2 0.501 0.047 10.718 0.000
##
## Variances
## X1 1.000 0.000 999.000 999.000
## X2 1.000 0.000 999.000 999.000
##
## Residual Variances
## Y 0.463 0.042 10.912 0.000
##
##
## STDY Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Y ON
## X1 0.317 0.048 6.595 0.000
## X2 0.521 0.045 11.638 0.000
##
## X1 WITH
## X2 0.501 0.047 10.718 0.000
##
## Variances
## X1 1.000 0.000 999.000 999.000
## X2 1.000 0.000 999.000 999.000
##
## Residual Variances
## Y 0.463 0.042 10.912 0.000
##
##
## STD Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Y ON
## X1 0.277 0.043 6.454 0.000
## X2 0.439 0.041 10.603 0.000
##
## X1 WITH
## X2 108.576 15.139 7.172 0.000
##
## Variances
## X1 209.182 18.489 11.314 0.000
## X2 224.125 19.810 11.314 0.000
##
## Residual Variances
## Y 73.716 6.516 11.314 0.000
##
##
## R-SQUARE
##
## Observed Two-Tailed
## Variable Estimate S.E. Est./S.E. P-Value
##
## Y 0.537 0.042 12.681 0.000
##
##
## QUALITY OF NUMERICAL RESULTS
##
## Condition Number for the Information Matrix 0.829E-02
## (ratio of smallest to largest eigenvalue)
##
##
## CONFIDENCE INTERVALS OF MODEL RESULTS
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Y ON
## X1 0.166 0.193 0.206 0.277 0.347 0.361 0.387
## X2 0.333 0.358 0.371 0.439 0.507 0.520 0.546
##
## X1 WITH
## X2 69.582 78.904 83.673 108.576 133.480 138.249 147.571
##
## Variances
## X1 161.558 172.943 178.767 209.182 239.597 245.421 256.807
## X2 173.098 185.297 191.538 224.125 256.713 262.953 275.152
##
## Residual Variances
## Y 56.933 60.945 62.997 73.716 84.434 86.486 90.498
##
##
## CONFIDENCE INTERVALS OF STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Y ON
## X1 0.193 0.223 0.238 0.317 0.396 0.411 0.441
## X2 0.406 0.433 0.447 0.521 0.595 0.609 0.636
##
## X1 WITH
## X2 0.381 0.410 0.424 0.501 0.578 0.593 0.622
##
## Variances
## X1 1.000 1.000 1.000 1.000 1.000 1.000 1.000
## X2 1.000 1.000 1.000 1.000 1.000 1.000 1.000
##
## Residual Variances
## Y 0.353 0.379 0.393 0.463 0.532 0.546 0.572
##
##
## STDY Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Y ON
## X1 0.193 0.223 0.238 0.317 0.396 0.411 0.441
## X2 0.406 0.433 0.447 0.521 0.595 0.609 0.636
##
## X1 WITH
## X2 0.381 0.410 0.424 0.501 0.578 0.593 0.622
##
## Variances
## X1 1.000 1.000 1.000 1.000 1.000 1.000 1.000
## X2 1.000 1.000 1.000 1.000 1.000 1.000 1.000
##
## Residual Variances
## Y 0.353 0.379 0.393 0.463 0.532 0.546 0.572
##
##
## STD Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Y ON
## X1 0.166 0.193 0.206 0.277 0.347 0.361 0.387
## X2 0.333 0.358 0.371 0.439 0.507 0.520 0.546
##
## X1 WITH
## X2 69.582 78.904 83.673 108.576 133.480 138.249 147.571
##
## Variances
## X1 161.558 172.943 178.767 209.182 239.597 245.421 256.807
## X2 173.098 185.297 191.538 224.125 256.713 262.953 275.152
##
## Residual Variances
## Y 56.933 60.945 62.997 73.716 84.434 86.486 90.498
##
##
## RESIDUAL OUTPUT
##
##
## ESTIMATED MODEL AND RESIDUALS (OBSERVED - ESTIMATED)
##
##
## Model Estimated Covariances/Correlations/Residual Correlations
## Y X1 X2
## ________ ________ ________
## Y 159.384
## X1 105.588 209.182
## X2 128.500 108.577 224.125
##
##
## Residuals for Covariances/Correlations/Residual Correlations
## Y X1 X2
## ________ ________ ________
## Y -0.009
## X1 -0.002 -0.003
## X2 -0.003 -0.002 -0.004
##
##
## Standardized Residuals (z-scores) for Covariances/Correlations/Residual Corr
## Y X1 X2
## ________ ________ ________
## Y 999.000
## X1 999.000 999.000
## X2 999.000 999.000 999.000
##
##
## Normalized Residuals for Covariances/Correlations/Residual Correlations
## Y X1 X2
## ________ ________ ________
## Y -0.001
## X1 0.000 0.000
## X2 0.000 0.000 0.000
##
##
## Beginning Time: 12:19:09
## Ending Time: 12:19:09
## Elapsed Time: 00:00:00
##
##
##
## MUTHEN & MUTHEN
## 3463 Stoner Ave.
## Los Angeles, CA 90066
##
## Tel: (310) 391-9971
## Fax: (310) 391-8971
## Web: www.StatModel.com
## Support: Support@StatModel.com
##
## Copyright (c) 1998-2019 Muthen & Muthen3.2.2 Regression of Y on X1 and X2 - sample correlation matrix and SDs as input
TITLE: this is an example of an overidentified
path analysis model from Cnudde and McCrone (1966)
DATA: FILE IS "data\CORR.DAT";
TYPE IS CORRELATION STDEVIATIONS;
NOBSERVATIONS ARE 116;
VARIABLE: NAMES ARE X Y1 Y2 Y3;
MODEL: Y1 ON Y2;
Y2 ON X;
Y3 ON Y1 Y2;
MODEL INDIRECT: Y3 IND Y2 X;
Y3 IND Y1 Y2;
OUTPUT: SAMPSTAT STANDARDIZED RESIDUAL CINTERVAL;## Mplus VERSION 8.4
## MUTHEN & MUTHEN
## 06/10/2021 12:19 PM
##
## INPUT INSTRUCTIONS
##
## TITLE: this is an example of an overidentified
## path analysis model from Cnudde and McCrone (1966)
## DATA: FILE IS "data\CORR.DAT";
## TYPE IS CORRELATION STDEVIATIONS;
## NOBSERVATIONS ARE 116;
## VARIABLE: NAMES ARE X Y1 Y2 Y3;
## MODEL: Y1 ON Y2;
## Y2 ON X;
## Y3 ON Y1 Y2;
## MODEL INDIRECT: Y3 IND Y2 X;
## Y3 IND Y1 Y2;
## OUTPUT: SAMPSTAT STANDARDIZED RESIDUAL CINTERVAL;
##
##
##
## 1 ERROR(S) FOUND IN THE INPUT INSTRUCTIONS
##
##
##
## this is an example of an overidentified
## path analysis model from Cnudde and McCrone (1966)
##
## SUMMARY OF ANALYSIS
##
## Number of groups 1
## Number of observations 116
##
## Number of dependent variables 3
## Number of independent variables 1
## Number of continuous latent variables 0
##
## Observed dependent variables
##
## Continuous
## Y1 Y2 Y3
##
## Observed independent variables
## X
##
##
## Estimator ML
## Information matrix EXPECTED
## Maximum number of iterations 1000
## Convergence criterion 0.500D-04
## Maximum number of steepest descent iterations 20
##
## Input data file(s)
## data\CORR.DAT
##
## Input data format FREE
##
##
## SAMPLE STATISTICS
##
##
## SAMPLE STATISTICS
##
##
## Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 X
## ________ ________ ________ ________
## Y1 108.368
## Y2 100.404 225.000
## Y3 99.750 164.065 176.624
## X 71.334 152.323 118.683 189.338
##
##
## THE MODEL ESTIMATION TERMINATED NORMALLY
##
##
##
## MODEL FIT INFORMATION
##
## Number of Free Parameters 7
##
## Loglikelihood
##
## H0 Value -1223.560
## H1 Value -1222.871
##
## Information Criteria
##
## Akaike (AIC) 2461.120
## Bayesian (BIC) 2480.395
## Sample-Size Adjusted BIC 2458.268
## (n* = (n + 2) / 24)
##
## Chi-Square Test of Model Fit
##
## Value 1.377
## Degrees of Freedom 2
## P-Value 0.5023
##
## RMSEA (Root Mean Square Error Of Approximation)
##
## Estimate 0.000
## 90 Percent C.I. 0.000 0.165
## Probability RMSEA <= .05 0.594
##
## CFI/TLI
##
## CFI 1.000
## TLI 1.000
##
## Chi-Square Test of Model Fit for the Baseline Model
##
## Value 310.802
## Degrees of Freedom 6
## P-Value 0.0000
##
## SRMR (Standardized Root Mean Square Residual)
##
## Value 0.016
##
##
##
## MODEL RESULTS
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Y1 ON
## Y2 0.446 0.049 9.042 0.000
##
## Y2 ON
## X 0.805 0.068 11.779 0.000
##
## Y3 ON
## Y1 0.417 0.079 5.291 0.000
## Y2 0.543 0.055 9.913 0.000
##
## Residual Variances
## Y1 63.016 8.274 7.616 0.000
## Y2 101.571 13.337 7.616 0.000
## Y3 45.517 5.977 7.616 0.000
##
##
## STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Y1 ON
## Y2 0.643 0.054 11.807 0.000
##
## Y2 ON
## X 0.738 0.042 17.456 0.000
##
## Y3 ON
## Y1 0.327 0.062 5.316 0.000
## Y2 0.613 0.056 10.862 0.000
##
## Residual Variances
## Y1 0.587 0.070 8.375 0.000
## Y2 0.455 0.062 7.297 0.000
## Y3 0.260 0.042 6.260 0.000
##
##
## STDY Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Y1 ON
## Y2 0.643 0.054 11.807 0.000
##
## Y2 ON
## X 0.054 0.003 16.514 0.000
##
## Y3 ON
## Y1 0.327 0.062 5.316 0.000
## Y2 0.613 0.056 10.862 0.000
##
## Residual Variances
## Y1 0.587 0.070 8.375 0.000
## Y2 0.455 0.062 7.297 0.000
## Y3 0.260 0.042 6.260 0.000
##
##
## STD Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Y1 ON
## Y2 0.446 0.049 9.042 0.000
##
## Y2 ON
## X 0.805 0.068 11.779 0.000
##
## Y3 ON
## Y1 0.417 0.079 5.291 0.000
## Y2 0.543 0.055 9.913 0.000
##
## Residual Variances
## Y1 63.016 8.274 7.616 0.000
## Y2 101.571 13.337 7.616 0.000
## Y3 45.517 5.977 7.616 0.000
##
##
## R-SQUARE
##
## Observed Two-Tailed
## Variable Estimate S.E. Est./S.E. P-Value
##
## Y1 0.413 0.070 5.903 0.000
## Y2 0.545 0.062 8.728 0.000
## Y3 0.740 0.042 17.822 0.000
##
##
## QUALITY OF NUMERICAL RESULTS
##
## Condition Number for the Information Matrix 0.203E-01
## (ratio of smallest to largest eigenvalue)
##
##
## TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
##
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Effects from X to Y3
##
## Indirect 0.437 0.058 7.585 0.000
##
## Effects from Y2 to Y3
##
## Indirect 0.186 0.041 4.566 0.000
##
##
## STANDARDIZED TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
##
##
## STDYX Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Effects from X to Y3
##
## Indirect 0.452 0.052 8.762 0.000
##
## Effects from Y2 to Y3
##
## Indirect 0.210 0.043 4.878 0.000
##
##
## STDY Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Effects from X to Y3
##
## Indirect 0.033 0.004 9.169 0.000
##
## Effects from Y2 to Y3
##
## Indirect 0.210 0.043 4.878 0.000
##
##
## STD Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## Effects from X to Y3
##
## Indirect 0.437 0.058 7.585 0.000
##
## Effects from Y2 to Y3
##
## Indirect 0.186 0.041 4.566 0.000
##
##
##
## CONFIDENCE INTERVALS OF MODEL RESULTS
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Y1 ON
## Y2 0.319 0.350 0.365 0.446 0.527 0.543 0.573
##
## Y2 ON
## X 0.629 0.671 0.692 0.805 0.917 0.938 0.980
##
## Y3 ON
## Y1 0.214 0.263 0.288 0.417 0.547 0.572 0.621
## Y2 0.402 0.436 0.453 0.543 0.633 0.650 0.684
##
## Residual Variances
## Y1 41.702 46.798 49.404 63.016 76.627 79.233 84.329
## Y2 67.218 75.431 79.632 101.571 123.510 127.711 135.924
## Y3 30.122 33.802 35.685 45.517 55.348 57.231 60.911
##
##
## CONFIDENCE INTERVALS OF STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Y1 ON
## Y2 0.503 0.536 0.553 0.643 0.733 0.750 0.783
##
## Y2 ON
## X 0.629 0.655 0.668 0.738 0.808 0.821 0.847
##
## Y3 ON
## Y1 0.169 0.206 0.226 0.327 0.428 0.448 0.485
## Y2 0.467 0.502 0.520 0.613 0.706 0.723 0.758
##
## Residual Variances
## Y1 0.406 0.449 0.471 0.587 0.702 0.724 0.767
## Y2 0.295 0.333 0.353 0.455 0.558 0.578 0.616
## Y3 0.153 0.179 0.192 0.260 0.328 0.341 0.367
##
##
## STDY Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Y1 ON
## Y2 0.503 0.536 0.553 0.643 0.733 0.750 0.783
##
## Y2 ON
## X 0.045 0.047 0.049 0.054 0.059 0.060 0.062
##
## Y3 ON
## Y1 0.169 0.206 0.226 0.327 0.428 0.448 0.485
## Y2 0.467 0.502 0.520 0.613 0.706 0.723 0.758
##
## Residual Variances
## Y1 0.406 0.449 0.471 0.587 0.702 0.724 0.767
## Y2 0.295 0.333 0.353 0.455 0.558 0.578 0.616
## Y3 0.153 0.179 0.192 0.260 0.328 0.341 0.367
##
##
## STD Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Y1 ON
## Y2 0.319 0.350 0.365 0.446 0.527 0.543 0.573
##
## Y2 ON
## X 0.629 0.671 0.692 0.805 0.917 0.938 0.980
##
## Y3 ON
## Y1 0.214 0.263 0.288 0.417 0.547 0.572 0.621
## Y2 0.402 0.436 0.453 0.543 0.633 0.650 0.684
##
## Residual Variances
## Y1 41.702 46.798 49.404 63.016 76.627 79.233 84.329
## Y2 67.218 75.431 79.632 101.571 123.510 127.711 135.924
## Y3 30.122 33.802 35.685 45.517 55.348 57.231 60.911
##
##
## CONFIDENCE INTERVALS OF TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
##
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Effects from X to Y3
##
## Indirect 0.288 0.324 0.342 0.437 0.531 0.550 0.585
##
## Effects from Y2 to Y3
##
## Indirect 0.081 0.106 0.119 0.186 0.253 0.266 0.291
##
##
## CONFIDENCE INTERVALS OF STANDARDIZED TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
##
##
## STDYX Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Effects from X to Y3
##
## Indirect 0.319 0.351 0.367 0.452 0.537 0.553 0.585
##
## Effects from Y2 to Y3
##
## Indirect 0.099 0.126 0.139 0.210 0.281 0.295 0.321
##
##
## STDY Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Effects from X to Y3
##
## Indirect 0.024 0.026 0.027 0.033 0.039 0.040 0.042
##
## Effects from Y2 to Y3
##
## Indirect 0.099 0.126 0.139 0.210 0.281 0.295 0.321
##
##
## STD Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## Effects from X to Y3
##
## Indirect 0.288 0.324 0.342 0.437 0.531 0.550 0.585
##
## Effects from Y2 to Y3
##
## Indirect 0.081 0.106 0.119 0.186 0.253 0.266 0.291
##
##
##
## RESIDUAL OUTPUT
##
##
## ESTIMATED MODEL AND RESIDUALS (OBSERVED - ESTIMATED)
##
##
## Model Estimated Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 X
## ________ ________ ________ ________
## Y1 107.434
## Y2 99.538 223.059
## Y3 98.889 162.650 175.101
## X 67.387 151.010 110.113 187.705
##
##
## Residuals for Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 X
## ________ ________ ________ ________
## Y1 0.000
## Y2 0.001 0.001
## Y3 0.000 0.001 0.001
## X 3.332 0.000 7.547 0.000
##
##
## Standardized Residuals (z-scores) for Covariances/Correlations/Residual Corr
## Y1 Y2 Y3 X
## ________ ________ ________ ________
## Y1 0.008
## Y2 0.012 0.011
## Y3 0.006 0.010 0.011
## X 0.469 0.000 1.004 0.000
##
##
## Normalized Residuals for Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 X
## ________ ________ ________ ________
## Y1 0.000
## Y2 0.000 0.000
## Y3 0.000 0.000 0.000
## X 0.226 0.000 0.376 0.000
##
##
## Beginning Time: 12:19:09
## Ending Time: 12:19:10
## Elapsed Time: 00:00:01
##
##
##
## MUTHEN & MUTHEN
## 3463 Stoner Ave.
## Los Angeles, CA 90066
##
## Tel: (310) 391-9971
## Fax: (310) 391-8971
## Web: www.StatModel.com
## Support: Support@StatModel.com
##
## Copyright (c) 1998-2019 Muthen & Muthen3.2.3 Path analysis model - Wheaton et al. (1977) example
TITLE: Path analysis model - Wheaton et al. (1977) example
DATA: FILE IS "data\Wheaton.txt";
TYPE IS COVARIANCE;
NOBSERVATIONS ARE 932;
VARIABLE: NAMES ARE X1 X2 X3 X4;
MODEL: X3 ON X1 X2;
X4 ON X1 X2;
X1 WITH X2;
! estimate covariance between X1 and X2
X1*; X2*;
! estimate variances of X1 and X2
X3 WITH X4@0;
! fix the residual covariance between X3 and X4 at 0.
! otherwise, it is a free parameter by default
OUTPUT: SAMPSTAT STANDARDIZED RESIDUAL CINTERVAL;## Mplus VERSION 8.4
## MUTHEN & MUTHEN
## 06/10/2021 12:19 PM
##
## INPUT INSTRUCTIONS
##
## TITLE: Path analysis model - Wheaton et al. (1977) example
##
## DATA: FILE IS "data\Wheaton.txt";
## TYPE IS COVARIANCE;
## NOBSERVATIONS ARE 932;
## VARIABLE: NAMES ARE X1 X2 X3 X4;
## MODEL: X3 ON X1 X2;
## X4 ON X1 X2;
## X1 WITH X2;
## ! estimate covariance between X1 and X2
## X1*; X2*;
## ! estimate variances of X1 and X2
## X3 WITH X4@0;
## ! fix the residual covariance between X3 and X4 at 0.
## ! otherwise, it is a free parameter by default
## OUTPUT: SAMPSTAT STANDARDIZED RESIDUAL CINTERVAL;
##
##
##
## 1 ERROR(S) FOUND IN THE INPUT INSTRUCTIONS
##
##
##
## Path analysis model - Wheaton et al. (1977) example
##
## SUMMARY OF ANALYSIS
##
## Number of groups 1
## Number of observations 932
##
## Number of dependent variables 2
## Number of independent variables 2
## Number of continuous latent variables 0
##
## Observed dependent variables
##
## Continuous
## X3 X4
##
## Observed independent variables
## X1 X2
##
##
## Estimator ML
## Information matrix EXPECTED
## Maximum number of iterations 1000
## Convergence criterion 0.500D-04
## Maximum number of steepest descent iterations 20
##
## Input data file(s)
## data\Wheaton.txt
##
## Input data format FREE
##
##
## SAMPLE STATISTICS
##
##
## SAMPLE STATISTICS
##
##
## Covariances/Correlations/Residual Correlations
## X3 X4 X1 X2
## ________ ________ ________ ________
## X3 12.585
## X4 7.375 10.036
## X1 7.417 5.077 12.892
## X2 5.205 5.091 7.064 9.237
##
##
## THE MODEL ESTIMATION TERMINATED NORMALLY
##
##
##
## MODEL FIT INFORMATION
##
## Number of Free Parameters 9
##
## Loglikelihood
##
## H0 Value -9145.166
## H1 Value -8994.559
##
## Information Criteria
##
## Akaike (AIC) 18308.331
## Bayesian (BIC) 18351.867
## Sample-Size Adjusted BIC 18323.284
## (n* = (n + 2) / 24)
##
## Chi-Square Test of Model Fit
##
## Value 301.214
## Degrees of Freedom 1
## P-Value 0.0000
##
## RMSEA (Root Mean Square Error Of Approximation)
##
## Estimate 0.568
## 90 Percent C.I. 0.515 0.622
## Probability RMSEA <= .05 0.000
##
## CFI/TLI
##
## CFI 0.711
## TLI 0.000
##
## Chi-Square Test of Model Fit for the Baseline Model
##
## Value 1044.799
## Degrees of Freedom 5
## P-Value 0.0000
##
## SRMR (Standardized Root Mean Square Residual)
##
## Value 0.112
##
##
##
## MODEL RESULTS
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## X3 ON
## X1 0.459 0.034 13.490 0.000
## X2 0.213 0.040 5.291 0.000
##
## X4 ON
## X1 0.158 0.032 4.975 0.000
## X2 0.430 0.038 11.467 0.000
##
## X1 WITH
## X2 7.056 0.425 16.590 0.000
##
## X3 WITH
## X4 0.000 0.000 999.000 999.000
##
## Variances
## X1 12.878 0.597 21.587 0.000
## X2 9.227 0.427 21.587 0.000
##
## Residual Variances
## X3 8.067 0.374 21.587 0.000
## X4 7.035 0.326 21.587 0.000
##
##
## STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## X3 ON
## X1 0.464 0.032 14.393 0.000
## X2 0.182 0.034 5.333 0.000
##
## X4 ON
## X1 0.179 0.036 5.016 0.000
## X2 0.413 0.034 12.063 0.000
##
## X1 WITH
## X2 0.647 0.019 34.016 0.000
##
## X3 WITH
## X4 0.000 0.000 999.000 999.000
##
## Variances
## X1 1.000 0.000 999.000 999.000
## X2 1.000 0.000 999.000 999.000
##
## Residual Variances
## X3 0.642 0.025 25.499 0.000
## X4 0.702 0.025 27.951 0.000
##
##
## STDY Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## X3 ON
## X1 0.464 0.032 14.393 0.000
## X2 0.182 0.034 5.333 0.000
##
## X4 ON
## X1 0.179 0.036 5.016 0.000
## X2 0.413 0.034 12.063 0.000
##
## X1 WITH
## X2 0.647 0.019 34.016 0.000
##
## X3 WITH
## X4 0.000 0.000 999.000 999.000
##
## Variances
## X1 1.000 0.000 999.000 999.000
## X2 1.000 0.000 999.000 999.000
##
## Residual Variances
## X3 0.642 0.025 25.499 0.000
## X4 0.702 0.025 27.951 0.000
##
##
## STD Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## X3 ON
## X1 0.459 0.034 13.490 0.000
## X2 0.213 0.040 5.291 0.000
##
## X4 ON
## X1 0.158 0.032 4.975 0.000
## X2 0.430 0.038 11.467 0.000
##
## X1 WITH
## X2 7.056 0.425 16.590 0.000
##
## X3 WITH
## X4 0.000 0.000 999.000 999.000
##
## Variances
## X1 12.878 0.597 21.587 0.000
## X2 9.227 0.427 21.587 0.000
##
## Residual Variances
## X3 8.067 0.374 21.587 0.000
## X4 7.035 0.326 21.587 0.000
##
##
## R-SQUARE
##
## Observed Two-Tailed
## Variable Estimate S.E. Est./S.E. P-Value
##
## X3 0.358 0.025 14.240 0.000
## X4 0.298 0.025 11.878 0.000
##
##
## QUALITY OF NUMERICAL RESULTS
##
## Condition Number for the Information Matrix 0.161E-01
## (ratio of smallest to largest eigenvalue)
##
##
## CONFIDENCE INTERVALS OF MODEL RESULTS
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## X3 ON
## X1 0.371 0.392 0.403 0.459 0.515 0.525 0.546
## X2 0.109 0.134 0.147 0.213 0.279 0.291 0.316
##
## X4 ON
## X1 0.076 0.096 0.106 0.158 0.210 0.220 0.240
## X2 0.334 0.357 0.369 0.430 0.492 0.504 0.527
##
## X1 WITH
## X2 5.961 6.223 6.357 7.056 7.756 7.890 8.152
##
## X3 WITH
## X4 0.000 0.000 0.000 0.000 0.000 0.000 0.000
##
## Variances
## X1 11.342 11.709 11.897 12.878 13.860 14.047 14.415
## X2 8.126 8.389 8.524 9.227 9.930 10.065 10.328
##
## Residual Variances
## X3 7.104 7.334 7.452 8.067 8.681 8.799 9.029
## X4 6.196 6.397 6.499 7.035 7.572 7.674 7.875
##
##
## CONFIDENCE INTERVALS OF STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## X3 ON
## X1 0.381 0.401 0.411 0.464 0.517 0.528 0.547
## X2 0.094 0.115 0.126 0.182 0.238 0.249 0.270
##
## X4 ON
## X1 0.087 0.109 0.120 0.179 0.238 0.249 0.271
## X2 0.325 0.346 0.357 0.413 0.469 0.480 0.501
##
## X1 WITH
## X2 0.598 0.610 0.616 0.647 0.679 0.685 0.696
##
## X3 WITH
## X4 0.000 0.000 0.000 0.000 0.000 0.000 0.000
##
## Variances
## X1 1.000 1.000 1.000 1.000 1.000 1.000 1.000
## X2 1.000 1.000 1.000 1.000 1.000 1.000 1.000
##
## Residual Variances
## X3 0.577 0.592 0.600 0.642 0.683 0.691 0.706
## X4 0.637 0.653 0.660 0.702 0.743 0.751 0.766
##
##
## STDY Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## X3 ON
## X1 0.381 0.401 0.411 0.464 0.517 0.528 0.547
## X2 0.094 0.115 0.126 0.182 0.238 0.249 0.270
##
## X4 ON
## X1 0.087 0.109 0.120 0.179 0.238 0.249 0.271
## X2 0.325 0.346 0.357 0.413 0.469 0.480 0.501
##
## X1 WITH
## X2 0.598 0.610 0.616 0.647 0.679 0.685 0.696
##
## X3 WITH
## X4 0.000 0.000 0.000 0.000 0.000 0.000 0.000
##
## Variances
## X1 1.000 1.000 1.000 1.000 1.000 1.000 1.000
## X2 1.000 1.000 1.000 1.000 1.000 1.000 1.000
##
## Residual Variances
## X3 0.577 0.592 0.600 0.642 0.683 0.691 0.706
## X4 0.637 0.653 0.660 0.702 0.743 0.751 0.766
##
##
## STD Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## X3 ON
## X1 0.371 0.392 0.403 0.459 0.515 0.525 0.546
## X2 0.109 0.134 0.147 0.213 0.279 0.291 0.316
##
## X4 ON
## X1 0.076 0.096 0.106 0.158 0.210 0.220 0.240
## X2 0.334 0.357 0.369 0.430 0.492 0.504 0.527
##
## X1 WITH
## X2 5.961 6.223 6.357 7.056 7.756 7.890 8.152
##
## X3 WITH
## X4 0.000 0.000 0.000 0.000 0.000 0.000 0.000
##
## Variances
## X1 11.342 11.709 11.897 12.878 13.860 14.047 14.415
## X2 8.126 8.389 8.524 9.227 9.930 10.065 10.328
##
## Residual Variances
## X3 7.104 7.334 7.452 8.067 8.681 8.799 9.029
## X4 6.196 6.397 6.499 7.035 7.572 7.674 7.875
##
##
## RESIDUAL OUTPUT
##
##
## ESTIMATED MODEL AND RESIDUALS (OBSERVED - ESTIMATED)
##
##
## Model Estimated Covariances/Correlations/Residual Correlations
## X3 X4 X1 X2
## ________ ________ ________ ________
## X3 12.572
## X4 3.408 10.025
## X1 7.409 5.072 12.878
## X2 5.199 5.086 7.056 9.227
##
##
## Residuals for Covariances/Correlations/Residual Correlations
## X3 X4 X1 X2
## ________ ________ ________ ________
## X3 0.000
## X4 3.959 0.000
## X1 0.000 0.000 0.000
## X2 0.000 0.000 0.000 0.000
##
##
## Standardized Residuals (z-scores) for Covariances/Correlations/Residual Corr
## X3 X4 X1 X2
## ________ ________ ________ ________
## X3 999.000
## X4 12.122 999.000
## X1 999.000 999.000 999.000
## X2 999.000 999.000 999.000 999.000
##
##
## Normalized Residuals for Covariances/Correlations/Residual Correlations
## X3 X4 X1 X2
## ________ ________ ________ ________
## X3 0.000
## X4 9.001 0.000
## X1 0.000 0.000 0.000
## X2 0.000 0.000 0.000 0.000
##
##
## Beginning Time: 12:19:10
## Ending Time: 12:19:10
## Elapsed Time: 00:00:00
##
##
##
## MUTHEN & MUTHEN
## 3463 Stoner Ave.
## Los Angeles, CA 90066
##
## Tel: (310) 391-9971
## Fax: (310) 391-8971
## Web: www.StatModel.com
## Support: Support@StatModel.com
##
## Copyright (c) 1998-2019 Muthen & Muthen3.2.4 Use raw data as input
TITLE: Path analysis model - Wheaton et al. (1977) example
raw data
DATA: FILE IS "data\wheaton-generated.dat";
FORMAT IS F8 F8 F8 F8 F8 F8;
! you can also use 6F8;
VARIABLE: NAMES ARE anomia67 powles67 anomia71 powles71 educ sei;
USEVARIABLES ARE anomia67 powles67 anomia71 powles71;
MODEL: anomia71 ON anomia67 powles67;
powles71 ON anomia67 powles67;
anomia67 WITH powles67;
! estimate covariance
anomia67*; powles67*;
! estimate variances
anomia71 WITH powles71@0;
! fix the residual covariance at 0.
OUTPUT: SAMPSTAT STANDARDIZED RESIDUAL CINTERVAL;## Mplus VERSION 8.4
## MUTHEN & MUTHEN
## 06/10/2021 12:19 PM
##
## INPUT INSTRUCTIONS
##
## TITLE: Path analysis model - Wheaton et al. (1977) example
## raw data
## DATA: FILE IS "data\wheaton-generated.dat";
## FORMAT IS F8 F8 F8 F8 F8 F8;
## ! you can also use 6F8;
## VARIABLE: NAMES ARE anomia67 powles67 anomia71 powles71 educ sei;
## USEVARIABLES ARE anomia67 powles67 anomia71 powles71;
## MODEL: anomia71 ON anomia67 powles67;
## powles71 ON anomia67 powles67;
## anomia67 WITH powles67;
## ! estimate covariance
## anomia67*; powles67*;
## ! estimate variances
## anomia71 WITH powles71@0;
## ! fix the residual covariance at 0.
## OUTPUT: SAMPSTAT STANDARDIZED RESIDUAL CINTERVAL;
##
##
##
## 1 ERROR(S) FOUND IN THE INPUT INSTRUCTIONS
##
##
##
## Path analysis model - Wheaton et al. (1977) example
## raw data
##
## SUMMARY OF ANALYSIS
##
## Number of groups 1
## Number of observations 932
##
## Number of dependent variables 2
## Number of independent variables 2
## Number of continuous latent variables 0
##
## Observed dependent variables
##
## Continuous
## ANOMIA71 POWLES71
##
## Observed independent variables
## ANOMIA67 POWLES67
##
##
## Estimator ML
## Information matrix OBSERVED
## Maximum number of iterations 1000
## Convergence criterion 0.500D-04
## Maximum number of steepest descent iterations 20
##
## Input data file(s)
## data\wheaton-generated.dat
##
## Input data format
## (F8 F8 F8 F8 F8 F8)
##
##
## SAMPLE STATISTICS
##
##
## SAMPLE STATISTICS
##
##
## Means
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## 3.557 3.079 3.559 3.087
##
##
## Covariances
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## ANOMIA71 12.572
## POWLES71 7.366 10.025
## ANOMIA67 7.409 5.070 12.877
## POWLES67 5.199 5.086 7.056 9.227
##
##
## Correlations
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## ANOMIA71 1.000
## POWLES71 0.656 1.000
## ANOMIA67 0.582 0.446 1.000
## POWLES67 0.483 0.529 0.647 1.000
##
##
## UNIVARIATE SAMPLE STATISTICS
##
##
## UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
##
## Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
## Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
##
## ANOMIA71 3.557 0.074 -7.410 0.11% 0.630 2.590 3.510
## 932.000 12.572 0.087 15.630 0.11% 4.270 6.730
## POWLES71 3.079 -0.036 -6.680 0.11% 0.410 2.190 3.120
## 932.000 10.025 -0.212 13.630 0.11% 3.950 5.700
## ANOMIA67 3.559 0.115 -7.910 0.11% 0.700 2.530 3.340
## 932.000 12.877 0.134 15.080 0.11% 4.170 6.570
## POWLES67 3.087 -0.030 -6.360 0.11% 0.490 2.330 3.110
## 932.000 9.227 0.086 13.550 0.11% 3.870 5.610
##
##
## THE MODEL ESTIMATION TERMINATED NORMALLY
##
##
##
## MODEL FIT INFORMATION
##
## Number of Free Parameters 13
##
## Loglikelihood
##
## H0 Value -9145.171
## H1 Value -8994.594
##
## Information Criteria
##
## Akaike (AIC) 18316.342
## Bayesian (BIC) 18379.227
## Sample-Size Adjusted BIC 18337.940
## (n* = (n + 2) / 24)
##
## Chi-Square Test of Model Fit
##
## Value 301.153
## Degrees of Freedom 1
## P-Value 0.0000
##
## RMSEA (Root Mean Square Error Of Approximation)
##
## Estimate 0.567
## 90 Percent C.I. 0.515 0.622
## Probability RMSEA <= .05 0.000
##
## CFI/TLI
##
## CFI 0.711
## TLI 0.000
##
## Chi-Square Test of Model Fit for the Baseline Model
##
## Value 1044.669
## Degrees of Freedom 5
## P-Value 0.0000
##
## SRMR (Standardized Root Mean Square Residual)
##
## Value 0.094
##
##
##
## MODEL RESULTS
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## ANOMIA71 ON
## ANOMIA67 0.459 0.034 13.489 0.000
## POWLES67 0.213 0.040 5.291 0.000
##
## POWLES71 ON
## ANOMIA67 0.158 0.032 4.970 0.000
## POWLES67 0.430 0.038 11.470 0.000
##
## ANOMIA67 WITH
## POWLES67 7.057 0.425 16.589 0.000
##
## ANOMIA71 WITH
## POWLES71 0.000 0.000 999.000 999.000
##
## Means
## ANOMIA67 3.559 0.118 30.274 0.000
## POWLES67 3.087 0.100 31.021 0.000
##
## Intercepts
## ANOMIA71 1.268 0.139 9.136 0.000
## POWLES71 1.188 0.130 9.171 0.000
##
## Variances
## ANOMIA67 12.878 0.597 21.586 0.000
## POWLES67 9.228 0.427 21.586 0.000
##
## Residual Variances
## ANOMIA71 8.067 0.374 21.588 0.000
## POWLES71 7.035 0.326 21.588 0.000
##
##
## STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## ANOMIA71 ON
## ANOMIA67 0.464 0.032 14.391 0.000
## POWLES67 0.182 0.034 5.332 0.000
##
## POWLES71 ON
## ANOMIA67 0.179 0.036 5.011 0.000
## POWLES67 0.413 0.034 12.066 0.000
##
## ANOMIA67 WITH
## POWLES67 0.647 0.019 34.019 0.000
##
## ANOMIA71 WITH
## POWLES71 0.000 0.000 999.000 999.000
##
## Means
## ANOMIA67 0.992 0.040 24.787 0.000
## POWLES67 1.016 0.040 25.192 0.000
##
## Intercepts
## ANOMIA71 0.358 0.044 8.164 0.000
## POWLES71 0.375 0.046 8.214 0.000
##
## Variances
## ANOMIA67 1.000 0.000 999.000 999.000
## POWLES67 1.000 0.000 999.000 999.000
##
## Residual Variances
## ANOMIA71 0.642 0.025 25.499 0.000
## POWLES71 0.702 0.025 27.951 0.000
##
##
## STDY Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## ANOMIA71 ON
## ANOMIA67 0.464 0.032 14.391 0.000
## POWLES67 0.182 0.034 5.332 0.000
##
## POWLES71 ON
## ANOMIA67 0.179 0.036 5.011 0.000
## POWLES67 0.413 0.034 12.066 0.000
##
## ANOMIA67 WITH
## POWLES67 0.647 0.019 34.019 0.000
##
## ANOMIA71 WITH
## POWLES71 0.000 0.000 999.000 999.000
##
## Means
## ANOMIA67 0.992 0.040 24.787 0.000
## POWLES67 1.016 0.040 25.192 0.000
##
## Intercepts
## ANOMIA71 0.358 0.044 8.164 0.000
## POWLES71 0.375 0.046 8.214 0.000
##
## Variances
## ANOMIA67 1.000 0.000 999.000 999.000
## POWLES67 1.000 0.000 999.000 999.000
##
## Residual Variances
## ANOMIA71 0.642 0.025 25.499 0.000
## POWLES71 0.702 0.025 27.951 0.000
##
##
## STD Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## ANOMIA71 ON
## ANOMIA67 0.459 0.034 13.489 0.000
## POWLES67 0.213 0.040 5.291 0.000
##
## POWLES71 ON
## ANOMIA67 0.158 0.032 4.970 0.000
## POWLES67 0.430 0.038 11.470 0.000
##
## ANOMIA67 WITH
## POWLES67 7.057 0.425 16.589 0.000
##
## ANOMIA71 WITH
## POWLES71 0.000 0.000 999.000 999.000
##
## Means
## ANOMIA67 3.559 0.118 30.274 0.000
## POWLES67 3.087 0.100 31.021 0.000
##
## Intercepts
## ANOMIA71 1.268 0.139 9.136 0.000
## POWLES71 1.188 0.130 9.171 0.000
##
## Variances
## ANOMIA67 12.878 0.597 21.586 0.000
## POWLES67 9.228 0.427 21.586 0.000
##
## Residual Variances
## ANOMIA71 8.067 0.374 21.588 0.000
## POWLES71 7.035 0.326 21.588 0.000
##
##
## R-SQUARE
##
## Observed Two-Tailed
## Variable Estimate S.E. Est./S.E. P-Value
##
## ANOMIA71 0.358 0.025 14.239 0.000
## POWLES71 0.298 0.025 11.878 0.000
##
##
## QUALITY OF NUMERICAL RESULTS
##
## Condition Number for the Information Matrix 0.719E-02
## (ratio of smallest to largest eigenvalue)
##
##
## CONFIDENCE INTERVALS OF MODEL RESULTS
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## ANOMIA71 ON
## ANOMIA67 0.371 0.392 0.403 0.459 0.515 0.525 0.546
## POWLES67 0.109 0.134 0.146 0.213 0.279 0.291 0.316
##
## POWLES71 ON
## ANOMIA67 0.076 0.096 0.106 0.158 0.210 0.220 0.240
## POWLES67 0.334 0.357 0.369 0.430 0.492 0.504 0.527
##
## ANOMIA67 WITH
## POWLES67 5.961 6.223 6.357 7.057 7.757 7.891 8.153
##
## ANOMIA71 WITH
## POWLES71 0.000 0.000 0.000 0.000 0.000 0.000 0.000
##
## Means
## ANOMIA67 3.256 3.328 3.365 3.559 3.752 3.789 3.862
## POWLES67 2.830 2.892 2.923 3.087 3.250 3.282 3.343
##
## Intercepts
## ANOMIA71 0.910 0.996 1.039 1.268 1.496 1.540 1.625
## POWLES71 0.855 0.934 0.975 1.188 1.402 1.442 1.522
##
## Variances
## ANOMIA67 11.342 11.709 11.897 12.878 13.860 14.048 14.415
## POWLES67 8.127 8.390 8.524 9.228 9.931 10.066 10.329
##
## Residual Variances
## ANOMIA71 7.104 7.335 7.452 8.067 8.682 8.799 9.030
## POWLES71 6.196 6.397 6.499 7.035 7.571 7.674 7.875
##
##
## CONFIDENCE INTERVALS OF STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## ANOMIA71 ON
## ANOMIA67 0.381 0.401 0.411 0.464 0.517 0.528 0.547
## POWLES67 0.094 0.115 0.126 0.182 0.238 0.249 0.270
##
## POWLES71 ON
## ANOMIA67 0.087 0.109 0.120 0.179 0.238 0.249 0.271
## POWLES67 0.325 0.346 0.357 0.413 0.469 0.480 0.501
##
## ANOMIA67 WITH
## POWLES67 0.598 0.610 0.616 0.647 0.679 0.685 0.696
##
## ANOMIA71 WITH
## POWLES71 0.000 0.000 0.000 0.000 0.000 0.000 0.000
##
## Means
## ANOMIA67 0.889 0.913 0.926 0.992 1.057 1.070 1.095
## POWLES67 0.912 0.937 0.950 1.016 1.082 1.095 1.120
##
## Intercepts
## ANOMIA71 0.245 0.272 0.285 0.358 0.430 0.443 0.470
## POWLES71 0.258 0.286 0.300 0.375 0.451 0.465 0.493
##
## Variances
## ANOMIA67 1.000 1.000 1.000 1.000 1.000 1.000 1.000
## POWLES67 1.000 1.000 1.000 1.000 1.000 1.000 1.000
##
## Residual Variances
## ANOMIA71 0.577 0.592 0.600 0.642 0.683 0.691 0.706
## POWLES71 0.637 0.653 0.660 0.702 0.743 0.751 0.766
##
##
## STDY Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## ANOMIA71 ON
## ANOMIA67 0.381 0.401 0.411 0.464 0.517 0.528 0.547
## POWLES67 0.094 0.115 0.126 0.182 0.238 0.249 0.270
##
## POWLES71 ON
## ANOMIA67 0.087 0.109 0.120 0.179 0.238 0.249 0.271
## POWLES67 0.325 0.346 0.357 0.413 0.469 0.480 0.501
##
## ANOMIA67 WITH
## POWLES67 0.598 0.610 0.616 0.647 0.679 0.685 0.696
##
## ANOMIA71 WITH
## POWLES71 0.000 0.000 0.000 0.000 0.000 0.000 0.000
##
## Means
## ANOMIA67 0.889 0.913 0.926 0.992 1.057 1.070 1.095
## POWLES67 0.912 0.937 0.950 1.016 1.082 1.095 1.120
##
## Intercepts
## ANOMIA71 0.245 0.272 0.285 0.358 0.430 0.443 0.470
## POWLES71 0.258 0.286 0.300 0.375 0.451 0.465 0.493
##
## Variances
## ANOMIA67 1.000 1.000 1.000 1.000 1.000 1.000 1.000
## POWLES67 1.000 1.000 1.000 1.000 1.000 1.000 1.000
##
## Residual Variances
## ANOMIA71 0.577 0.592 0.600 0.642 0.683 0.691 0.706
## POWLES71 0.637 0.653 0.660 0.702 0.743 0.751 0.766
##
##
## STD Standardization
##
## Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
##
## ANOMIA71 ON
## ANOMIA67 0.371 0.392 0.403 0.459 0.515 0.525 0.546
## POWLES67 0.109 0.134 0.146 0.213 0.279 0.291 0.316
##
## POWLES71 ON
## ANOMIA67 0.076 0.096 0.106 0.158 0.210 0.220 0.240
## POWLES67 0.334 0.357 0.369 0.430 0.492 0.504 0.527
##
## ANOMIA67 WITH
## POWLES67 5.961 6.223 6.357 7.057 7.757 7.891 8.153
##
## ANOMIA71 WITH
## POWLES71 0.000 0.000 0.000 0.000 0.000 0.000 0.000
##
## Means
## ANOMIA67 3.256 3.328 3.365 3.559 3.752 3.789 3.862
## POWLES67 2.830 2.892 2.923 3.087 3.250 3.282 3.343
##
## Intercepts
## ANOMIA71 0.910 0.996 1.039 1.268 1.496 1.540 1.625
## POWLES71 0.855 0.934 0.975 1.188 1.402 1.442 1.522
##
## Variances
## ANOMIA67 11.342 11.709 11.897 12.878 13.860 14.048 14.415
## POWLES67 8.127 8.390 8.524 9.228 9.931 10.066 10.329
##
## Residual Variances
## ANOMIA71 7.104 7.335 7.452 8.067 8.682 8.799 9.030
## POWLES71 6.196 6.397 6.499 7.035 7.571 7.674 7.875
##
##
## RESIDUAL OUTPUT
##
##
## ESTIMATED MODEL AND RESIDUALS (OBSERVED - ESTIMATED)
##
##
## Model Estimated Means
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## 3.557 3.079 3.559 3.087
##
##
## Residuals for Means
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## 0.000 0.000 0.000 0.000
##
##
## Standardized Residuals (z-scores) for Means
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## 0.000 0.000 0.000 0.000
##
##
## Normalized Residuals for Means
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## 0.000 0.000 0.000 0.000
##
##
## Model Estimated Covariances
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## ANOMIA71 12.572
## POWLES71 3.408 10.025
## ANOMIA67 7.409 5.071 12.878
## POWLES67 5.200 5.086 7.057 9.228
##
##
## Model Estimated Correlations
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## ANOMIA71 1.000
## POWLES71 0.304 1.000
## ANOMIA67 0.582 0.446 1.000
## POWLES67 0.483 0.529 0.647 1.000
##
##
## Residuals for Covariances
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## ANOMIA71 0.000
## POWLES71 3.959 0.000
## ANOMIA67 0.000 0.000 -0.001
## POWLES67 0.000 0.000 -0.001 0.000
##
##
## Residuals for Correlations
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## ANOMIA71 0.000
## POWLES71 0.353 0.000
## ANOMIA67 0.000 0.000 0.000
## POWLES67 0.000 0.000 0.000 0.000
##
##
## Standardized Residuals (z-scores) for Covariances
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## ANOMIA71 999.000
## POWLES71 12.122 0.048
## ANOMIA67 999.000 999.000 999.000
## POWLES67 999.000 999.000 999.000 999.000
##
##
## Normalized Residuals for Covariances
## ANOMIA71 POWLES71 ANOMIA67 POWLES67
## ________ ________ ________ ________
## ANOMIA71 0.000
## POWLES71 9.000 0.000
## ANOMIA67 -0.001 -0.001 -0.001
## POWLES67 -0.001 0.000 -0.001 -0.001
##
##
## Beginning Time: 12:19:10
## Ending Time: 12:19:10
## Elapsed Time: 00:00:00
##
##
##
## MUTHEN & MUTHEN
## 3463 Stoner Ave.
## Los Angeles, CA 90066
##
## Tel: (310) 391-9971
## Fax: (310) 391-8971
## Web: www.StatModel.com
## Support: Support@StatModel.com
##
## Copyright (c) 1998-2019 Muthen & Muthen