Chapter 8 Latent Growth Models
8.1 Syntax - R
library(lavaan); library(semPlot)8.1.1 Linear latent growth models without means
LGROWTH.lower <- '
40.628
37.741 53.568
40.052 48.500 60.778
50.643 63.169 70.200 107.869'
LGROWTH.cov <- getCov(LGROWTH.lower, names = paste("Y", 1:4, sep=""))
lgm.linear.model <- '
F1 =~ 1*Y1 + 1*Y2 + 1*Y3 + 1*Y4
F2 =~ 0*Y1 + 1*Y2 + 3*Y3 + 5*Y4
F1 ~~ F2'
lgm.linear.fit <- cfa(lgm.linear.model, sample.cov = LGROWTH.cov, sample.nobs = 204)
summary(lgm.linear.fit, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE) ## lavaan 0.6-8 ended normally after 44 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 7
##
## Number of observations 204
##
## Model Test User Model:
##
## Test statistic 10.114
## Degrees of freedom 3
## P-value (Chi-square) 0.018
##
## Model Test Baseline Model:
##
## Test statistic 824.610
## Degrees of freedom 6
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.991
## Tucker-Lewis Index (TLI) 0.983
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -2428.904
## Loglikelihood unrestricted model (H1) -2423.846
##
## Akaike (AIC) 4871.807
## Bayesian (BIC) 4895.034
## Sample-size adjusted Bayesian (BIC) 4872.856
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.108
## 90 Percent confidence interval - lower 0.040
## 90 Percent confidence interval - upper 0.184
## P-value RMSEA <= 0.05 0.075
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.056
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## F1 =~
## Y1 1.000 5.712 0.889
## Y2 1.000 5.712 0.816
## Y3 1.000 5.712 0.704
## Y4 1.000 5.712 0.570
## F2 =~
## Y1 0.000 0.000 0.000
## Y2 1.000 0.855 0.122
## Y3 3.000 2.566 0.316
## Y4 5.000 4.276 0.427
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## F1 ~~
## F2 3.322 0.575 5.773 0.000 0.680 0.680
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Y1 8.657 1.373 6.303 0.000 8.657 0.210
## .Y2 9.001 1.174 7.665 0.000 9.001 0.184
## .Y3 6.684 1.164 5.742 0.000 6.684 0.102
## .Y4 16.322 2.673 6.107 0.000 16.322 0.162
## F1 32.630 3.806 8.574 0.000 1.000 1.000
## F2 0.731 0.168 4.341 0.000 1.000 1.000
##
## R-Square:
## Estimate
## Y1 0.790
## Y2 0.816
## Y3 0.898
## Y4 0.838# If the "growth" function is used, the latent factor means are also estimated (although for this example, there is no information on means).
lgm.linear.fit2 <- growth(lgm.linear.model, sample.cov = LGROWTH.cov, sample.nobs = 204)
summary(lgm.linear.fit2, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE) ## lavaan 0.6-8 ended normally after 44 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 9
##
## Number of observations 204
##
## Model Test User Model:
##
## Test statistic 10.114
## Degrees of freedom 5
## P-value (Chi-square) 0.072
##
## Model Test Baseline Model:
##
## Test statistic 824.610
## Degrees of freedom 6
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.994
## Tucker-Lewis Index (TLI) 0.993
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -2428.904
## Loglikelihood unrestricted model (H1) -2423.846
##
## Akaike (AIC) 4875.807
## Bayesian (BIC) 4905.670
## Sample-size adjusted Bayesian (BIC) 4877.156
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.071
## 90 Percent confidence interval - lower 0.000
## 90 Percent confidence interval - upper 0.134
## P-value RMSEA <= 0.05 0.242
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.047
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## F1 =~
## Y1 1.000 5.712 0.889
## Y2 1.000 5.712 0.816
## Y3 1.000 5.712 0.704
## Y4 1.000 5.712 0.570
## F2 =~
## Y1 0.000 0.000 0.000
## Y2 1.000 0.855 0.122
## Y3 3.000 2.566 0.316
## Y4 5.000 4.276 0.427
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## F1 ~~
## F2 3.322 0.575 5.773 0.000 0.680 0.680
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Y1 0.000 0.000 0.000
## .Y2 0.000 0.000 0.000
## .Y3 0.000 0.000 0.000
## .Y4 0.000 0.000 0.000
## F1 0.000 0.432 0.000 1.000 0.000 0.000
## F2 0.000 0.086 0.000 1.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Y1 8.657 1.373 6.303 0.000 8.657 0.210
## .Y2 9.001 1.174 7.665 0.000 9.001 0.184
## .Y3 6.684 1.164 5.742 0.000 6.684 0.102
## .Y4 16.322 2.673 6.107 0.000 16.322 0.162
## F1 32.630 3.806 8.574 0.000 1.000 1.000
## F2 0.731 0.168 4.341 0.000 1.000 1.000
##
## R-Square:
## Estimate
## Y1 0.790
## Y2 0.816
## Y3 0.898
## Y4 0.8388.1.2 Linear latent growth models with means
8.1.2.1 use the cfa() function
LGROWTH.means <- c(18.304, 25.819, 35.255, 46.593)
lgm.linear.with.mean.model <- '
F1 =~ 1*Y1 + 1*Y2 + 1*Y3 + 1*Y4
F2 =~ 0*Y1 + 1*Y2 + 3*Y3 + 5*Y4
F1 ~~ F2
F1 ~ 1
F2 ~ 1
Y1 ~ 0*1
Y2 ~ 0*1
Y3 ~ 0*1
Y4 ~ 0*1'
lgm.linear.with.mean.fit <- cfa(lgm.linear.with.mean.model, sample.cov = LGROWTH.cov, sample.mean = LGROWTH.means, sample.nobs = 204)
summary(lgm.linear.with.mean.fit, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE) ## lavaan 0.6-8 ended normally after 75 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 9
##
## Number of observations 204
##
## Model Test User Model:
##
## Test statistic 56.800
## Degrees of freedom 5
## P-value (Chi-square) 0.000
##
## Model Test Baseline Model:
##
## Test statistic 824.610
## Degrees of freedom 6
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.937
## Tucker-Lewis Index (TLI) 0.924
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -2452.247
## Loglikelihood unrestricted model (H1) -2423.846
##
## Akaike (AIC) 4922.493
## Bayesian (BIC) 4952.356
## Sample-size adjusted Bayesian (BIC) 4923.841
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.225
## 90 Percent confidence interval - lower 0.175
## 90 Percent confidence interval - upper 0.280
## P-value RMSEA <= 0.05 0.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.072
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## F1 =~
## Y1 1.000 5.587 0.868
## Y2 1.000 5.587 0.784
## Y3 1.000 5.587 0.693
## Y4 1.000 5.587 0.557
## F2 =~
## Y1 0.000 0.000 0.000
## Y2 1.000 0.805 0.113
## Y3 3.000 2.415 0.300
## Y4 5.000 4.025 0.401
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## F1 ~~
## F2 3.599 0.586 6.140 0.000 0.800 0.800
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## F1 19.029 0.430 44.287 0.000 3.406 3.406
## F2 5.499 0.086 63.760 0.000 6.832 6.832
## .Y1 0.000 0.000 0.000
## .Y2 0.000 0.000 0.000
## .Y3 0.000 0.000 0.000
## .Y4 0.000 0.000 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Y1 10.236 1.572 6.513 0.000 10.236 0.247
## .Y2 11.711 1.442 8.119 0.000 11.711 0.231
## .Y3 6.323 1.193 5.302 0.000 6.323 0.097
## .Y4 17.238 2.727 6.321 0.000 17.238 0.171
## F1 31.218 3.793 8.230 0.000 1.000 1.000
## F2 0.648 0.172 3.766 0.000 1.000 1.000
##
## R-Square:
## Estimate
## Y1 0.753
## Y2 0.769
## Y3 0.903
## Y4 0.8298.1.2.2 use the growth() function
Technically, the growth() function is almost identical to the sem() function. But a mean structure is automatically assumed, and the observed intercepts are fixed to zero by default, while the latent variable intercepts/means are freely estimated.
lgm.linear.model <- '
F1 =~ 1*Y1 + 1*Y2 + 1*Y3 + 1*Y4
F2 =~ 0*Y1 + 1*Y2 + 3*Y3 + 5*Y4
F1 ~~ F2'
lgm.linear.with.mean.fit2 <- growth(lgm.linear.model, sample.cov = LGROWTH.cov, sample.mean = LGROWTH.means, sample.nobs = 204)
summary(lgm.linear.with.mean.fit2, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE) ## lavaan 0.6-8 ended normally after 75 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 9
##
## Number of observations 204
##
## Model Test User Model:
##
## Test statistic 56.800
## Degrees of freedom 5
## P-value (Chi-square) 0.000
##
## Model Test Baseline Model:
##
## Test statistic 824.610
## Degrees of freedom 6
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.937
## Tucker-Lewis Index (TLI) 0.924
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -2452.247
## Loglikelihood unrestricted model (H1) -2423.846
##
## Akaike (AIC) 4922.493
## Bayesian (BIC) 4952.356
## Sample-size adjusted Bayesian (BIC) 4923.841
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.225
## 90 Percent confidence interval - lower 0.175
## 90 Percent confidence interval - upper 0.280
## P-value RMSEA <= 0.05 0.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.072
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## F1 =~
## Y1 1.000 5.587 0.868
## Y2 1.000 5.587 0.784
## Y3 1.000 5.587 0.693
## Y4 1.000 5.587 0.557
## F2 =~
## Y1 0.000 0.000 0.000
## Y2 1.000 0.805 0.113
## Y3 3.000 2.415 0.300
## Y4 5.000 4.025 0.401
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## F1 ~~
## F2 3.599 0.586 6.140 0.000 0.800 0.800
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Y1 0.000 0.000 0.000
## .Y2 0.000 0.000 0.000
## .Y3 0.000 0.000 0.000
## .Y4 0.000 0.000 0.000
## F1 19.029 0.430 44.287 0.000 3.406 3.406
## F2 5.499 0.086 63.760 0.000 6.832 6.832
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .Y1 10.236 1.572 6.513 0.000 10.236 0.247
## .Y2 11.711 1.442 8.119 0.000 11.711 0.231
## .Y3 6.323 1.193 5.302 0.000 6.323 0.097
## .Y4 17.238 2.727 6.321 0.000 17.238 0.171
## F1 31.218 3.793 8.230 0.000 1.000 1.000
## F2 0.648 0.172 3.766 0.000 1.000 1.000
##
## R-Square:
## Estimate
## Y1 0.753
## Y2 0.769
## Y3 0.903
## Y4 0.829semPaths(lgm.linear.with.mean.fit2)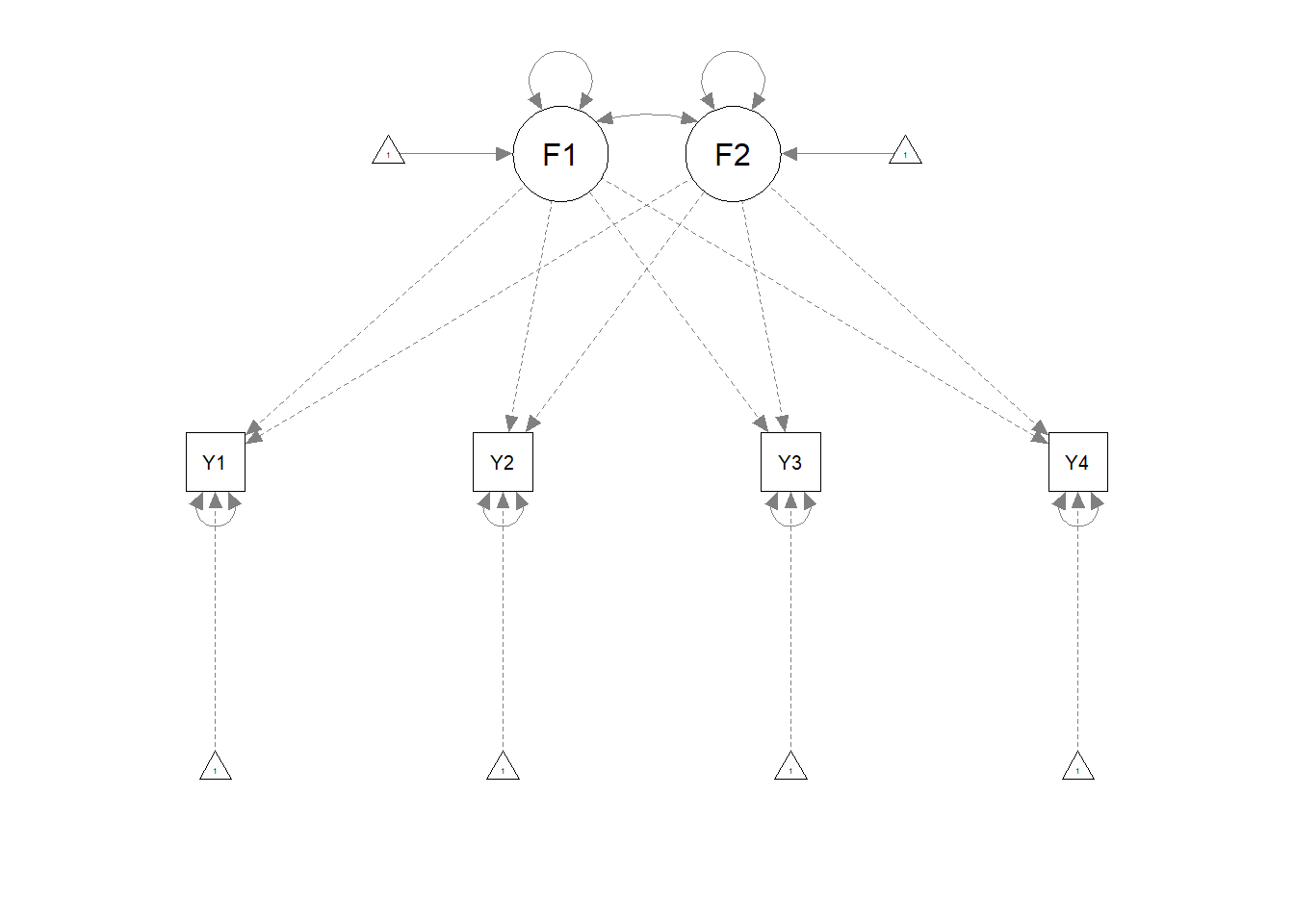
8.1.3 Linear latent growth models with predictors
LGROWTHP.lower <- '
40.628
37.741 53.568
40.052 48.500 60.778
50.643 63.169 70.200 107.869
8.949 10.493 9.430 12.843 7.290'
LGROWTHP.cov <- getCov(LGROWTHP.lower, names = c(paste("Y", 1:4, sep=""), "X1"))
lgm.linear.with.predictor.model <- '
F1 =~ 1*Y1 + 1*Y2 + 1*Y3 + 1*Y4
F2 =~ 0*Y1 + 1*Y2 + 3*Y3 + 5*Y4
F1 ~ X1
F2 ~ X1
F1 ~~ F2
X1 ~~ X1'
lgm.linear.with.predictor.fit <- cfa(lgm.linear.with.predictor.model, sample.cov = LGROWTHP.cov, sample.nobs = 204)
summary(lgm.linear.with.predictor.fit, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE) ## lavaan 0.6-8 ended normally after 46 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 10
##
## Number of observations 204
##
## Model Test User Model:
##
## Test statistic 14.308
## Degrees of freedom 5
## P-value (Chi-square) 0.014
##
## Model Test Baseline Model:
##
## Test statistic 900.650
## Degrees of freedom 10
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.990
## Tucker-Lewis Index (TLI) 0.979
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -2884.566
## Loglikelihood unrestricted model (H1) -2877.412
##
## Akaike (AIC) 5789.132
## Bayesian (BIC) 5822.313
## Sample-size adjusted Bayesian (BIC) 5790.630
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.096
## 90 Percent confidence interval - lower 0.039
## 90 Percent confidence interval - upper 0.155
## P-value RMSEA <= 0.05 0.083
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.051
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## F1 =~
## Y1 1.000 5.721 0.889
## Y2 1.000 5.721 0.819
## Y3 1.000 5.721 0.704
## Y4 1.000 5.721 0.570
## F2 =~
## Y1 0.000 0.000 0.000
## Y2 1.000 0.850 0.122
## Y3 3.000 2.550 0.314
## Y4 5.000 4.250 0.424
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## F1 ~
## X1 1.248 0.135 9.277 0.000 0.218 0.588
## F2 ~
## X1 0.067 0.032 2.118 0.034 0.079 0.212
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .F1 ~~
## .F2 2.716 0.482 5.633 0.000 0.706 0.706
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## X1 7.254 0.718 10.100 0.000 7.254 1.000
## .Y1 8.725 1.331 6.553 0.000 8.725 0.210
## .Y2 8.718 1.128 7.731 0.000 8.718 0.179
## .Y3 6.830 1.173 5.824 0.000 6.830 0.103
## .Y4 16.558 2.692 6.151 0.000 16.558 0.165
## .F1 21.429 2.709 7.909 0.000 0.655 0.655
## .F2 0.690 0.165 4.177 0.000 0.955 0.955
##
## R-Square:
## Estimate
## Y1 0.790
## Y2 0.821
## Y3 0.897
## Y4 0.835
## F1 0.345
## F2 0.045semPaths(lgm.linear.with.predictor.fit)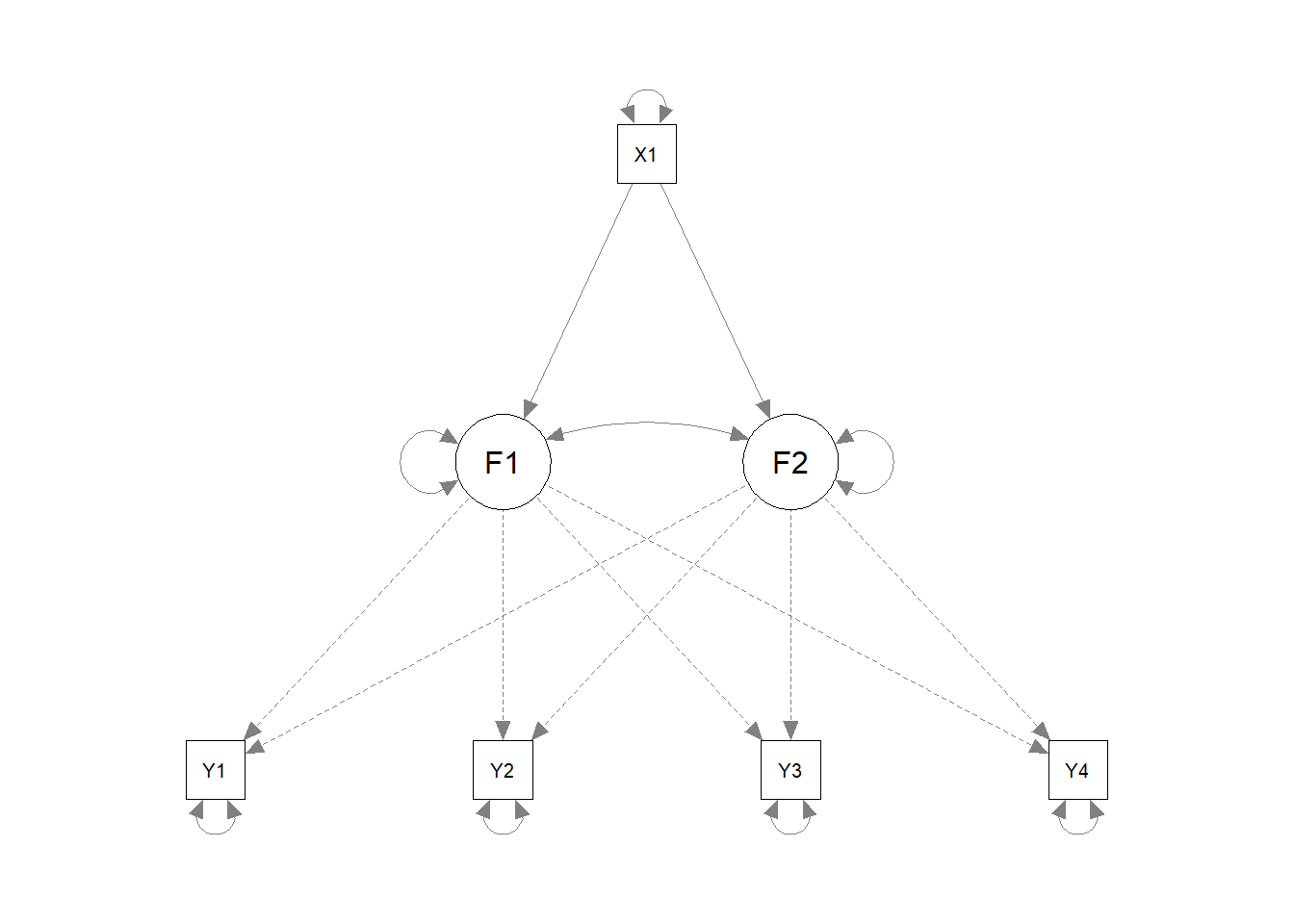
8.2 Syntax - Mplus
8.2.1 Linear latent growth models without means
TITLE: LATENT GROWTH MODEL -- LINEAR
DATA: FILE IS "data\LGROWTH.txt";
TYPE IS COVARIANCE;
NOBSERVATIONS IS 204;
VARIABLE: NAMES ARE Y1-Y4;
MODEL: F1 BY Y1@1 Y2@1 Y3@1 Y4@1;
F2 BY Y1@0 Y2@1 Y3@3 Y4@5;
F1 WITH F2;
OUTPUT: SAMP STDYX RES;## Mplus VERSION 8.4
## MUTHEN & MUTHEN
## 06/10/2021 12:20 PM
##
## INPUT INSTRUCTIONS
##
## TITLE: LATENT GROWTH MODEL -- LINEAR
## DATA: FILE IS "data\LGROWTH.txt";
## TYPE IS COVARIANCE;
## NOBSERVATIONS IS 204;
## VARIABLE: NAMES ARE Y1-Y4;
## MODEL: F1 BY Y1@1 Y2@1 Y3@1 Y4@1;
## F2 BY Y1@0 Y2@1 Y3@3 Y4@5;
## F1 WITH F2;
## OUTPUT: SAMP STDYX RES;
##
##
##
## 1 ERROR(S) FOUND IN THE INPUT INSTRUCTIONS
##
##
##
## LATENT GROWTH MODEL -- LINEAR
##
## SUMMARY OF ANALYSIS
##
## Number of groups 1
## Number of observations 204
##
## Number of dependent variables 4
## Number of independent variables 0
## Number of continuous latent variables 2
##
## Observed dependent variables
##
## Continuous
## Y1 Y2 Y3 Y4
##
## Continuous latent variables
## F1 F2
##
##
## Estimator ML
## Information matrix EXPECTED
## Maximum number of iterations 1000
## Convergence criterion 0.500D-04
## Maximum number of steepest descent iterations 20
##
## Input data file(s)
## data\LGROWTH.txt
##
## Input data format FREE
##
##
## SAMPLE STATISTICS
##
##
## SAMPLE STATISTICS
##
##
## Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 40.628
## Y2 37.741 53.568
## Y3 40.052 48.500 60.778
## Y4 50.643 63.169 70.200 107.869
##
##
## THE MODEL ESTIMATION TERMINATED NORMALLY
##
##
##
## MODEL FIT INFORMATION
##
## Number of Free Parameters 7
##
## Loglikelihood
##
## H0 Value -2428.904
## H1 Value -2423.846
##
## Information Criteria
##
## Akaike (AIC) 4871.807
## Bayesian (BIC) 4895.034
## Sample-Size Adjusted BIC 4872.856
## (n* = (n + 2) / 24)
##
## Chi-Square Test of Model Fit
##
## Value 10.114
## Degrees of Freedom 3
## P-Value 0.0176
##
## RMSEA (Root Mean Square Error Of Approximation)
##
## Estimate 0.108
## 90 Percent C.I. 0.040 0.184
## Probability RMSEA <= .05 0.075
##
## CFI/TLI
##
## CFI 0.991
## TLI 0.983
##
## Chi-Square Test of Model Fit for the Baseline Model
##
## Value 824.610
## Degrees of Freedom 6
## P-Value 0.0000
##
## SRMR (Standardized Root Mean Square Residual)
##
## Value 0.056
##
##
##
## MODEL RESULTS
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## F1 BY
## Y1 1.000 0.000 999.000 999.000
## Y2 1.000 0.000 999.000 999.000
## Y3 1.000 0.000 999.000 999.000
## Y4 1.000 0.000 999.000 999.000
##
## F2 BY
## Y1 0.000 0.000 999.000 999.000
## Y2 1.000 0.000 999.000 999.000
## Y3 3.000 0.000 999.000 999.000
## Y4 5.000 0.000 999.000 999.000
##
## F1 WITH
## F2 3.323 0.575 5.774 0.000
##
## Variances
## F1 32.629 3.806 8.574 0.000
## F2 0.732 0.169 4.341 0.000
##
## Residual Variances
## Y1 8.656 1.373 6.303 0.000
## Y2 9.000 1.174 7.665 0.000
## Y3 6.685 1.164 5.742 0.000
## Y4 16.322 2.673 6.107 0.000
##
##
## STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## F1 BY
## Y1 0.889 0.020 45.491 0.000
## Y2 0.816 0.020 41.138 0.000
## Y3 0.704 0.026 27.315 0.000
## Y4 0.570 0.028 20.445 0.000
##
## F2 BY
## Y1 0.000 0.000 999.000 999.000
## Y2 0.122 0.014 8.540 0.000
## Y3 0.316 0.034 9.426 0.000
## Y4 0.427 0.043 9.814 0.000
##
## F1 WITH
## F2 0.680 0.131 5.195 0.000
##
## Variances
## F1 1.000 0.000 999.000 999.000
## F2 1.000 0.000 999.000 999.000
##
## Residual Variances
## Y1 0.210 0.035 6.034 0.000
## Y2 0.184 0.026 7.167 0.000
## Y3 0.102 0.019 5.411 0.000
## Y4 0.162 0.028 5.822 0.000
##
##
## R-SQUARE
##
## Observed Two-Tailed
## Variable Estimate S.E. Est./S.E. P-Value
##
## Y1 0.790 0.035 22.745 0.000
## Y2 0.816 0.026 31.856 0.000
## Y3 0.898 0.019 47.879 0.000
## Y4 0.838 0.028 30.017 0.000
##
##
## QUALITY OF NUMERICAL RESULTS
##
## Condition Number for the Information Matrix 0.989E-01
## (ratio of smallest to largest eigenvalue)
##
##
## RESIDUAL OUTPUT
##
##
## ESTIMATED MODEL AND RESIDUALS (OBSERVED - ESTIMATED)
##
##
## Model Estimated Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 41.286
## Y2 35.952 49.006
## Y3 42.597 48.114 65.834
## Y4 49.242 56.223 70.184 100.467
##
##
## Residuals for Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 -0.857
## Y2 1.604 4.299
## Y3 -2.741 0.148 -5.354
## Y4 1.152 6.636 -0.328 6.874
##
##
## Standardized Residuals (z-scores) for Covariances/Correlations/Residual Corr
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 -0.809
## Y2 1.289 1.474
## Y3 999.000 0.104 999.000
## Y4 0.497 1.906 999.000 1.429
##
##
## Normalized Residuals for Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 -0.214
## Y2 0.384 0.815
## Y3 -0.617 0.028 -0.894
## Y4 0.198 0.964 -0.044 0.647
##
##
## Beginning Time: 12:20:11
## Ending Time: 12:20:11
## Elapsed Time: 00:00:00
##
##
##
## MUTHEN & MUTHEN
## 3463 Stoner Ave.
## Los Angeles, CA 90066
##
## Tel: (310) 391-9971
## Fax: (310) 391-8971
## Web: www.StatModel.com
## Support: Support@StatModel.com
##
## Copyright (c) 1998-2019 Muthen & Muthen8.2.2 Linear latent growth models with means
8.2.2.1 use factor analysis to specify growth models
TITLE: LATENT GROWTH MODEL - LINEAR WITH MEANS
DATA: FILE IS "data\LGROWTHM.txt";
TYPE IS COVARIANCE MEANS;
NOBSERVATIONS IS 204;
VARIABLE: NAMES ARE Y1-Y4;
MODEL: F1 BY Y1@1 Y2@1 Y3@1 Y4@1;
F2 BY Y1@0 Y2@1 Y3@3 Y4@5;
F1 WITH F2;
[F1* F2* Y1-Y4@0];
OUTPUT: SAMP STDYX RES;## Mplus VERSION 8.4
## MUTHEN & MUTHEN
## 06/10/2021 12:20 PM
##
## INPUT INSTRUCTIONS
##
## TITLE: LATENT GROWTH MODEL - LINEAR WITH MEANS
## DATA: FILE IS "data\LGROWTHM.txt";
## TYPE IS COVARIANCE MEANS;
## NOBSERVATIONS IS 204;
## VARIABLE: NAMES ARE Y1-Y4;
## MODEL: F1 BY Y1@1 Y2@1 Y3@1 Y4@1;
## F2 BY Y1@0 Y2@1 Y3@3 Y4@5;
## F1 WITH F2;
## [F1* F2* Y1-Y4@0];
## OUTPUT: SAMP STDYX RES;
##
##
##
## 1 ERROR(S) FOUND IN THE INPUT INSTRUCTIONS
##
##
##
## LATENT GROWTH MODEL - LINEAR WITH MEANS
##
## SUMMARY OF ANALYSIS
##
## Number of groups 1
## Number of observations 204
##
## Number of dependent variables 4
## Number of independent variables 0
## Number of continuous latent variables 2
##
## Observed dependent variables
##
## Continuous
## Y1 Y2 Y3 Y4
##
## Continuous latent variables
## F1 F2
##
##
## Estimator ML
## Information matrix EXPECTED
## Maximum number of iterations 1000
## Convergence criterion 0.500D-04
## Maximum number of steepest descent iterations 20
##
## Input data file(s)
## data\LGROWTHM.txt
##
## Input data format FREE
##
##
## SAMPLE STATISTICS
##
##
## SAMPLE STATISTICS
##
##
## Means/Intercepts/Thresholds
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## 18.304 25.819 35.255 46.593
##
##
## Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 40.628
## Y2 37.741 53.568
## Y3 40.052 48.500 60.778
## Y4 50.643 63.169 70.200 107.869
##
##
## THE MODEL ESTIMATION TERMINATED NORMALLY
##
##
##
## MODEL FIT INFORMATION
##
## Number of Free Parameters 9
##
## Loglikelihood
##
## H0 Value -2452.247
## H1 Value -2423.846
##
## Information Criteria
##
## Akaike (AIC) 4922.493
## Bayesian (BIC) 4952.356
## Sample-Size Adjusted BIC 4923.841
## (n* = (n + 2) / 24)
##
## Chi-Square Test of Model Fit
##
## Value 56.800
## Degrees of Freedom 5
## P-Value 0.0000
##
## RMSEA (Root Mean Square Error Of Approximation)
##
## Estimate 0.225
## 90 Percent C.I. 0.175 0.280
## Probability RMSEA <= .05 0.000
##
## CFI/TLI
##
## CFI 0.937
## TLI 0.924
##
## Chi-Square Test of Model Fit for the Baseline Model
##
## Value 824.610
## Degrees of Freedom 6
## P-Value 0.0000
##
## SRMR (Standardized Root Mean Square Residual)
##
## Value 0.072
##
##
##
## MODEL RESULTS
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## F1 BY
## Y1 1.000 0.000 999.000 999.000
## Y2 1.000 0.000 999.000 999.000
## Y3 1.000 0.000 999.000 999.000
## Y4 1.000 0.000 999.000 999.000
##
## F2 BY
## Y1 0.000 0.000 999.000 999.000
## Y2 1.000 0.000 999.000 999.000
## Y3 3.000 0.000 999.000 999.000
## Y4 5.000 0.000 999.000 999.000
##
## F1 WITH
## F2 3.599 0.586 6.140 0.000
##
## Means
## F1 19.029 0.430 44.287 0.000
## F2 5.499 0.086 63.760 0.000
##
## Intercepts
## Y1 0.000 0.000 999.000 999.000
## Y2 0.000 0.000 999.000 999.000
## Y3 0.000 0.000 999.000 999.000
## Y4 0.000 0.000 999.000 999.000
##
## Variances
## F1 31.218 3.793 8.230 0.000
## F2 0.648 0.172 3.766 0.000
##
## Residual Variances
## Y1 10.236 1.572 6.513 0.000
## Y2 11.711 1.442 8.119 0.000
## Y3 6.323 1.193 5.302 0.000
## Y4 17.238 2.727 6.321 0.000
##
##
## STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## F1 BY
## Y1 0.868 0.023 38.288 0.000
## Y2 0.784 0.023 34.541 0.000
## Y3 0.693 0.027 26.078 0.000
## Y4 0.557 0.028 19.571 0.000
##
## F2 BY
## Y1 0.000 0.000 999.000 999.000
## Y2 0.113 0.015 7.466 0.000
## Y3 0.300 0.037 8.163 0.000
## Y4 0.401 0.048 8.386 0.000
##
## F1 WITH
## F2 0.800 0.163 4.923 0.000
##
## Means
## F1 3.406 0.221 15.430 0.000
## F2 6.832 0.913 7.480 0.000
##
## Intercepts
## Y1 0.000 0.000 999.000 999.000
## Y2 0.000 0.000 999.000 999.000
## Y3 0.000 0.000 999.000 999.000
## Y4 0.000 0.000 999.000 999.000
##
## Variances
## F1 1.000 0.000 999.000 999.000
## F2 1.000 0.000 999.000 999.000
##
## Residual Variances
## Y1 0.247 0.039 6.277 0.000
## Y2 0.231 0.030 7.785 0.000
## Y3 0.097 0.019 5.057 0.000
## Y4 0.171 0.028 6.032 0.000
##
##
## R-SQUARE
##
## Observed Two-Tailed
## Variable Estimate S.E. Est./S.E. P-Value
##
## Y1 0.753 0.039 19.144 0.000
## Y2 0.769 0.030 25.969 0.000
## Y3 0.903 0.019 46.899 0.000
## Y4 0.829 0.028 29.185 0.000
##
##
## QUALITY OF NUMERICAL RESULTS
##
## Condition Number for the Information Matrix 0.461E-02
## (ratio of smallest to largest eigenvalue)
##
##
## RESIDUAL OUTPUT
##
##
## ESTIMATED MODEL AND RESIDUALS (OBSERVED - ESTIMATED)
##
##
## Model Estimated Means/Intercepts/Thresholds
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## 19.029 24.529 35.528 46.527
##
##
## Residuals for Means/Intercepts/Thresholds
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## -0.725 1.290 -0.273 0.066
##
##
## Standardized Residuals (z-scores) for Means/Intercepts/Thresholds
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## -6.231 5.652 999.000 0.251
##
##
## Normalized Residuals for Means/Intercepts/Thresholds
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## -1.630 2.524 -0.501 0.092
##
##
## Model Estimated Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 41.454
## Y2 34.817 50.776
## Y3 42.016 47.559 64.968
## Y4 49.214 56.053 69.731 100.646
##
##
## Residuals for Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 -1.025
## Y2 2.739 2.530
## Y3 -2.160 0.704 -4.488
## Y4 1.181 6.806 0.125 6.694
##
##
## Standardized Residuals (z-scores) for Covariances/Correlations/Residual Corr
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 -0.929
## Y2 2.069 0.882
## Y3 999.000 0.455 999.000
## Y4 0.492 1.917 0.338 1.380
##
##
## Normalized Residuals for Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 -0.256
## Y2 0.655 0.479
## Y3 -0.486 0.135 -0.749
## Y4 0.203 0.988 0.017 0.630
##
##
## Beginning Time: 12:20:12
## Ending Time: 12:20:12
## Elapsed Time: 00:00:00
##
##
##
## MUTHEN & MUTHEN
## 3463 Stoner Ave.
## Los Angeles, CA 90066
##
## Tel: (310) 391-9971
## Fax: (310) 391-8971
## Web: www.StatModel.com
## Support: Support@StatModel.com
##
## Copyright (c) 1998-2019 Muthen & Muthen8.2.2.2 use the | symbol to specify growth models
TITLE: LATENT GROWTH MODEL - LINEAR WITH MEANS
DATA: FILE IS "data\LGROWTHM.txt";
TYPE IS COVARIANCE MEANS;
NOBSERVATIONS IS 204;
VARIABLE: NAMES ARE Y1-Y4;
MODEL: i s | Y1@0 Y2@1 Y3@3 Y4@5;
OUTPUT: SAMP STDYX RES;## Mplus VERSION 8.4
## MUTHEN & MUTHEN
## 06/10/2021 12:20 PM
##
## INPUT INSTRUCTIONS
##
## TITLE: LATENT GROWTH MODEL - LINEAR WITH MEANS
## DATA: FILE IS "data\LGROWTHM.txt";
## TYPE IS COVARIANCE MEANS;
## NOBSERVATIONS IS 204;
## VARIABLE: NAMES ARE Y1-Y4;
## MODEL: i s | Y1@0 Y2@1 Y3@3 Y4@5;
## OUTPUT: SAMP STDYX RES;
##
##
##
## 1 ERROR(S) FOUND IN THE INPUT INSTRUCTIONS
##
##
##
## LATENT GROWTH MODEL - LINEAR WITH MEANS
##
## SUMMARY OF ANALYSIS
##
## Number of groups 1
## Number of observations 204
##
## Number of dependent variables 4
## Number of independent variables 0
## Number of continuous latent variables 2
##
## Observed dependent variables
##
## Continuous
## Y1 Y2 Y3 Y4
##
## Continuous latent variables
## I S
##
##
## Estimator ML
## Information matrix EXPECTED
## Maximum number of iterations 1000
## Convergence criterion 0.500D-04
## Maximum number of steepest descent iterations 20
##
## Input data file(s)
## data\LGROWTHM.txt
##
## Input data format FREE
##
##
## SAMPLE STATISTICS
##
##
## SAMPLE STATISTICS
##
##
## Means/Intercepts/Thresholds
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## 18.304 25.819 35.255 46.593
##
##
## Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 40.628
## Y2 37.741 53.568
## Y3 40.052 48.500 60.778
## Y4 50.643 63.169 70.200 107.869
##
##
## THE MODEL ESTIMATION TERMINATED NORMALLY
##
##
##
## MODEL FIT INFORMATION
##
## Number of Free Parameters 9
##
## Loglikelihood
##
## H0 Value -2452.247
## H1 Value -2423.846
##
## Information Criteria
##
## Akaike (AIC) 4922.493
## Bayesian (BIC) 4952.356
## Sample-Size Adjusted BIC 4923.841
## (n* = (n + 2) / 24)
##
## Chi-Square Test of Model Fit
##
## Value 56.800
## Degrees of Freedom 5
## P-Value 0.0000
##
## RMSEA (Root Mean Square Error Of Approximation)
##
## Estimate 0.225
## 90 Percent C.I. 0.175 0.280
## Probability RMSEA <= .05 0.000
##
## CFI/TLI
##
## CFI 0.937
## TLI 0.924
##
## Chi-Square Test of Model Fit for the Baseline Model
##
## Value 824.610
## Degrees of Freedom 6
## P-Value 0.0000
##
## SRMR (Standardized Root Mean Square Residual)
##
## Value 0.072
##
##
##
## MODEL RESULTS
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## I |
## Y1 1.000 0.000 999.000 999.000
## Y2 1.000 0.000 999.000 999.000
## Y3 1.000 0.000 999.000 999.000
## Y4 1.000 0.000 999.000 999.000
##
## S |
## Y1 0.000 0.000 999.000 999.000
## Y2 1.000 0.000 999.000 999.000
## Y3 3.000 0.000 999.000 999.000
## Y4 5.000 0.000 999.000 999.000
##
## S WITH
## I 3.599 0.586 6.140 0.000
##
## Means
## I 19.029 0.430 44.287 0.000
## S 5.499 0.086 63.760 0.000
##
## Intercepts
## Y1 0.000 0.000 999.000 999.000
## Y2 0.000 0.000 999.000 999.000
## Y3 0.000 0.000 999.000 999.000
## Y4 0.000 0.000 999.000 999.000
##
## Variances
## I 31.218 3.793 8.230 0.000
## S 0.648 0.172 3.766 0.000
##
## Residual Variances
## Y1 10.236 1.572 6.513 0.000
## Y2 11.711 1.442 8.119 0.000
## Y3 6.323 1.193 5.302 0.000
## Y4 17.238 2.727 6.321 0.000
##
##
## STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## I |
## Y1 0.868 0.023 38.288 0.000
## Y2 0.784 0.023 34.541 0.000
## Y3 0.693 0.027 26.078 0.000
## Y4 0.557 0.028 19.571 0.000
##
## S |
## Y1 0.000 0.000 999.000 999.000
## Y2 0.113 0.015 7.466 0.000
## Y3 0.300 0.037 8.163 0.000
## Y4 0.401 0.048 8.386 0.000
##
## S WITH
## I 0.800 0.163 4.923 0.000
##
## Means
## I 3.406 0.221 15.430 0.000
## S 6.832 0.913 7.480 0.000
##
## Intercepts
## Y1 0.000 0.000 999.000 999.000
## Y2 0.000 0.000 999.000 999.000
## Y3 0.000 0.000 999.000 999.000
## Y4 0.000 0.000 999.000 999.000
##
## Variances
## I 1.000 0.000 999.000 999.000
## S 1.000 0.000 999.000 999.000
##
## Residual Variances
## Y1 0.247 0.039 6.277 0.000
## Y2 0.231 0.030 7.785 0.000
## Y3 0.097 0.019 5.057 0.000
## Y4 0.171 0.028 6.032 0.000
##
##
## R-SQUARE
##
## Observed Two-Tailed
## Variable Estimate S.E. Est./S.E. P-Value
##
## Y1 0.753 0.039 19.144 0.000
## Y2 0.769 0.030 25.969 0.000
## Y3 0.903 0.019 46.899 0.000
## Y4 0.829 0.028 29.185 0.000
##
##
## QUALITY OF NUMERICAL RESULTS
##
## Condition Number for the Information Matrix 0.461E-02
## (ratio of smallest to largest eigenvalue)
##
##
## RESIDUAL OUTPUT
##
##
## ESTIMATED MODEL AND RESIDUALS (OBSERVED - ESTIMATED)
##
##
## Model Estimated Means/Intercepts/Thresholds
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## 19.029 24.529 35.528 46.527
##
##
## Residuals for Means/Intercepts/Thresholds
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## -0.725 1.290 -0.273 0.066
##
##
## Standardized Residuals (z-scores) for Means/Intercepts/Thresholds
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## -6.231 5.652 999.000 0.251
##
##
## Normalized Residuals for Means/Intercepts/Thresholds
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## -1.630 2.524 -0.501 0.092
##
##
## Model Estimated Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 41.454
## Y2 34.817 50.776
## Y3 42.016 47.559 64.968
## Y4 49.214 56.053 69.731 100.646
##
##
## Residuals for Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 -1.025
## Y2 2.739 2.530
## Y3 -2.160 0.704 -4.488
## Y4 1.181 6.806 0.125 6.694
##
##
## Standardized Residuals (z-scores) for Covariances/Correlations/Residual Corr
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 -0.929
## Y2 2.069 0.882
## Y3 999.000 0.455 999.000
## Y4 0.492 1.917 0.338 1.380
##
##
## Normalized Residuals for Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4
## ________ ________ ________ ________
## Y1 -0.256
## Y2 0.655 0.479
## Y3 -0.486 0.135 -0.749
## Y4 0.203 0.988 0.017 0.630
##
##
## Beginning Time: 12:20:12
## Ending Time: 12:20:12
## Elapsed Time: 00:00:00
##
##
##
## MUTHEN & MUTHEN
## 3463 Stoner Ave.
## Los Angeles, CA 90066
##
## Tel: (310) 391-9971
## Fax: (310) 391-8971
## Web: www.StatModel.com
## Support: Support@StatModel.com
##
## Copyright (c) 1998-2019 Muthen & Muthen8.2.3 Linear latent growth models with predictors
TITLE: LATENT GROWTH MODEL - LINEAR WITH PREDICTOR
DATA: FILE IS "data\LGROWTHP.txt";
TYPE IS COVARIANCE;
NOBSERVATIONS IS 204;
VARIABLE: NAMES ARE Y1-Y4 X1;
MODEL: F1 BY Y1-Y4@1;
F2 BY Y1@0 Y2@1 Y3@3 Y4@5;
F1 F2 ON X1;
F1 WITH F2;
X1*;
OUTPUT: SAMP STDYX RES;## Mplus VERSION 8.4
## MUTHEN & MUTHEN
## 06/10/2021 12:20 PM
##
## INPUT INSTRUCTIONS
##
## TITLE: LATENT GROWTH MODEL - LINEAR WITH PREDICTOR
## DATA: FILE IS "data\LGROWTHP.txt";
## TYPE IS COVARIANCE;
## NOBSERVATIONS IS 204;
## VARIABLE: NAMES ARE Y1-Y4 X1;
## MODEL: F1 BY Y1-Y4@1;
## F2 BY Y1@0 Y2@1 Y3@3 Y4@5;
## F1 F2 ON X1;
## F1 WITH F2;
## X1*;
## OUTPUT: SAMP STDYX RES;
##
##
##
## 1 ERROR(S) FOUND IN THE INPUT INSTRUCTIONS
##
##
##
## LATENT GROWTH MODEL - LINEAR WITH PREDICTOR
##
## SUMMARY OF ANALYSIS
##
## Number of groups 1
## Number of observations 204
##
## Number of dependent variables 4
## Number of independent variables 1
## Number of continuous latent variables 2
##
## Observed dependent variables
##
## Continuous
## Y1 Y2 Y3 Y4
##
## Observed independent variables
## X1
##
## Continuous latent variables
## F1 F2
##
##
## Estimator ML
## Information matrix EXPECTED
## Maximum number of iterations 1000
## Convergence criterion 0.500D-04
## Maximum number of steepest descent iterations 20
##
## Input data file(s)
## data\LGROWTHP.txt
##
## Input data format FREE
##
##
## SAMPLE STATISTICS
##
##
## SAMPLE STATISTICS
##
##
## Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4 X1
## ________ ________ ________ ________ ________
## Y1 40.628
## Y2 37.741 53.568
## Y3 40.052 48.500 60.778
## Y4 50.643 63.169 70.200 107.869
## X1 8.949 10.493 9.430 12.843 7.290
##
##
## THE MODEL ESTIMATION TERMINATED NORMALLY
##
##
##
## MODEL FIT INFORMATION
##
## Number of Free Parameters 10
##
## Loglikelihood
##
## H0 Value -2884.566
## H1 Value -2877.412
##
## Information Criteria
##
## Akaike (AIC) 5789.132
## Bayesian (BIC) 5822.313
## Sample-Size Adjusted BIC 5790.630
## (n* = (n + 2) / 24)
##
## Chi-Square Test of Model Fit
##
## Value 14.308
## Degrees of Freedom 5
## P-Value 0.0138
##
## RMSEA (Root Mean Square Error Of Approximation)
##
## Estimate 0.096
## 90 Percent C.I. 0.039 0.155
## Probability RMSEA <= .05 0.083
##
## CFI/TLI
##
## CFI 0.990
## TLI 0.979
##
## Chi-Square Test of Model Fit for the Baseline Model
##
## Value 900.650
## Degrees of Freedom 10
## P-Value 0.0000
##
## SRMR (Standardized Root Mean Square Residual)
##
## Value 0.051
##
##
##
## MODEL RESULTS
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## F1 BY
## Y1 1.000 0.000 999.000 999.000
## Y2 1.000 0.000 999.000 999.000
## Y3 1.000 0.000 999.000 999.000
## Y4 1.000 0.000 999.000 999.000
##
## F2 BY
## Y1 0.000 0.000 999.000 999.000
## Y2 1.000 0.000 999.000 999.000
## Y3 3.000 0.000 999.000 999.000
## Y4 5.000 0.000 999.000 999.000
##
## F1 ON
## X1 1.248 0.135 9.277 0.000
##
## F2 ON
## X1 0.067 0.032 2.118 0.034
##
## F1 WITH
## F2 2.716 0.482 5.633 0.000
##
## Variances
## X1 7.254 0.718 10.100 0.000
##
## Residual Variances
## Y1 8.725 1.331 6.553 0.000
## Y2 8.718 1.128 7.731 0.000
## Y3 6.830 1.173 5.824 0.000
## Y4 16.558 2.692 6.151 0.000
## F1 21.430 2.709 7.909 0.000
## F2 0.690 0.165 4.177 0.000
##
##
## STANDARDIZED MODEL RESULTS
##
##
## STDYX Standardization
##
## Two-Tailed
## Estimate S.E. Est./S.E. P-Value
##
## F1 BY
## Y1 0.889 0.019 46.560 0.000
## Y2 0.819 0.020 41.766 0.000
## Y3 0.704 0.026 27.395 0.000
## Y4 0.570 0.028 20.500 0.000
##
## F2 BY
## Y1 0.000 0.000 999.000 999.000
## Y2 0.122 0.014 8.453 0.000
## Y3 0.314 0.034 9.332 0.000
## Y4 0.424 0.044 9.714 0.000
##
## F1 ON
## X1 0.587 0.052 11.361 0.000
##
## F2 ON
## X1 0.212 0.099 2.139 0.032
##
## F1 WITH
## F2 0.706 0.150 4.717 0.000
##
## Variances
## X1 1.000 0.000 999.000 999.000
##
## Residual Variances
## Y1 0.210 0.034 6.207 0.000
## Y2 0.179 0.025 7.151 0.000
## Y3 0.103 0.019 5.478 0.000
## Y4 0.165 0.028 5.859 0.000
## F1 0.655 0.061 10.778 0.000
## F2 0.955 0.042 22.637 0.000
##
##
## R-SQUARE
##
## Observed Two-Tailed
## Variable Estimate S.E. Est./S.E. P-Value
##
## Y1 0.790 0.034 23.280 0.000
## Y2 0.821 0.025 32.888 0.000
## Y3 0.897 0.019 47.456 0.000
## Y4 0.835 0.028 29.727 0.000
##
## Latent Two-Tailed
## Variable Estimate S.E. Est./S.E. P-Value
##
## F1 0.345 0.061 5.680 0.000
## F2 0.045 0.042 1.070 0.285
##
##
## QUALITY OF NUMERICAL RESULTS
##
## Condition Number for the Information Matrix 0.530E-02
## (ratio of smallest to largest eigenvalue)
##
##
## RESIDUAL OUTPUT
##
##
## ESTIMATED MODEL AND RESIDUALS (OBSERVED - ESTIMATED)
##
##
## Model Estimated Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4 X1
## ________ ________ ________ ________ ________
## Y1 41.450
## Y2 36.048 48.811
## Y3 42.694 48.184 65.994
## Y4 49.340 56.275 70.144 100.572
## X1 9.052 9.538 10.511 11.483 7.254
##
##
## Residuals for Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4 X1
## ________ ________ ________ ________ ________
## Y1 -1.021
## Y2 1.508 4.494
## Y3 -2.838 0.078 -5.514
## Y4 1.055 6.585 -0.289 6.768
## X1 -0.147 0.903 -1.127 1.297 0.000
##
##
## Standardized Residuals (z-scores) for Covariances/Correlations/Residual Corr
## Y1 Y2 Y3 Y4 X1
## ________ ________ ________ ________ ________
## Y1 -0.973
## Y2 1.232 1.535
## Y3 999.000 0.056 999.000
## Y4 0.457 1.897 999.000 1.409
## X1 -0.550 1.346 999.000 1.618 0.011
##
##
## Normalized Residuals for Covariances/Correlations/Residual Correlations
## Y1 Y2 Y3 Y4 X1
## ________ ________ ________ ________ ________
## Y1 -0.255
## Y2 0.361 0.851
## Y3 -0.638 0.015 -0.921
## Y4 0.182 0.956 -0.039 0.637
## X1 -0.109 0.580 -0.701 0.604 0.000
##
##
## Beginning Time: 12:20:12
## Ending Time: 12:20:12
## Elapsed Time: 00:00:00
##
##
##
## MUTHEN & MUTHEN
## 3463 Stoner Ave.
## Los Angeles, CA 90066
##
## Tel: (310) 391-9971
## Fax: (310) 391-8971
## Web: www.StatModel.com
## Support: Support@StatModel.com
##
## Copyright (c) 1998-2019 Muthen & Muthen8.2.4 From Wang & Su (2013)
8.2.4.1 measurement invariance over time
TITLE: MEASUREMENT INVARIANCE OVER TIME
DATA: FILE IS "data\NELSSelfConcept3waves.dat";
FORMAT IS F7 F4 2F2 F11.4 39F2;
VARIABLE: NAMES ARE id status race gender weight
byconf1 byconf2 byconf3 byconf4 byconf5 byconf6 byconf7
byloc1 byloc2 byloc3 byloc4 byloc5 byloc6
f1conf1 f1conf2 f1conf3 f1conf4 f1conf5 f1conf6 f1conf7
f1loc1 f1loc2 f1loc3 f1loc4 f1loc5 f1loc6
f2conf1 f2conf2 f2conf3 f2conf4 f2conf5 f2conf6 f2conf7
f2loc1 f2loc2 f2loc3 f2loc4 f2loc5 f2loc6;
USEVARIABLES ARE byconf1-byconf4 byloc1-byloc4
f1conf1-f1conf4 f1loc1-f1loc4
f2conf1-f2conf4 f2loc1-f2loc4;
CATEGORICAL ARE byconf1-byconf4 byloc1-byloc4
f1conf1-f1conf4 f1loc1-f1loc4
f2conf1-f2conf4 f2loc1-f2loc4;
WEIGHT IS weight;
MISSING ARE race (99) gender (99) byconf1-f2loc6 (99);
ANALYSIS: ESTIMATOR=WLSMV;
OUTPUT: SAMPSTAT STANDARDIZED MODINDICES;
MODEL:
f1 BY byconf1@1;
f1 BY byconf2 (2);
f1 BY byconf3 (3);
f1 BY byconf4 (4);
f2 BY byloc1 (5);
f2 BY byloc2 (6);
f2 BY byloc3 (7);
f2 BY byloc4 (8);
f3 BY f1conf1@1;
f3 BY f1conf2 (2);
f3 BY f1conf3 (3);
f3 BY f1conf4 (4);
f4 BY f1loc1 (5);
f4 BY f1loc2 (6);
f4 BY f1loc3 (7);
f4 BY f1loc4 (8);
f5 BY f2conf1@1;
f5 BY f2conf2 (2);
f5 BY f2conf3 (3);
f5 BY f2conf4 (4);
f6 BY f2loc1 (5);
f6 BY f2loc2 (6);
f6 BY f2loc3 (7);
f6 BY f2loc4 (8);
[byconf1$1 f1conf1$1 f2conf1$1] (t1); ! constraining thresholds over time
[byconf1$2 f1conf1$2 f2conf1$2] (t2);
[byconf1$3 f1conf1$3 f2conf1$3] (t3);
[byconf2$1 f1conf2$1 f2conf2$1] (t4);
[byconf2$2 f1conf2$2 f2conf2$2] (t5);
[byconf2$3 f1conf2$3 f2conf2$3] (t6);
[byconf3$1 f1conf3$1 f2conf3$1] (t7);
[byconf3$2 f1conf3$2 f2conf3$2] (t8);
[byconf3$3 f1conf3$3 f2conf3$3] (t9);
[byconf4$1 f1conf4$1 f2conf4$1] (t10);
[byconf4$2 f1conf4$2 f2conf4$2] (t11);
[byconf4$3 f1conf4$3 f2conf4$3] (t12);
[byloc1$1 f1loc1$1 f2loc1$1] (t13);
[byloc1$2 f1loc1$2 f2loc1$2] (t14);
[byloc1$3 f1loc1$3 f2loc1$3] (t15);
[byloc2$1 f1loc2$1 f2loc2$1] (t16);
[byloc2$2 f1loc2$2 f2loc2$2] (t17);
[byloc2$3 f1loc2$3 f2loc2$3] (t18);
[byloc3$1 f1loc3$1 f2loc3$1] (t19);
[byloc3$2 f1loc3$2 f2loc3$2] (t20);
[byloc3$3 f1loc3$3 f2loc3$3] (t21);
[byloc4$1 f1loc4$1 f2loc4$1] (t22);
[byloc4$2 f1loc4$2 f2loc4$2] (t23);
[byloc4$3 f1loc4$3 f2loc4$3] (t24);8.2.4.2 measurement invariance over time and across gender groups
TITLE: MEASUREMENT INVARIANCE OVER TIME AND ACROSS GENDER GROUPS
DATA: FILE IS "data\NELSSelfConcept3waves.dat";
FORMAT IS F7 F4 2F2 F11.4 39F2;
VARIABLE: NAMES ARE id status race gender weight
byconf1 byconf2 byconf3 byconf4 byconf5 byconf6 byconf7
byloc1 byloc2 byloc3 byloc4 byloc5 byloc6
f1conf1 f1conf2 f1conf3 f1conf4 f1conf5 f1conf6 f1conf7
f1loc1 f1loc2 f1loc3 f1loc4 f1loc5 f1loc6
f2conf1 f2conf2 f2conf3 f2conf4 f2conf5 f2conf6 f2conf7
f2loc1 f2loc2 f2loc3 f2loc4 f2loc5 f2loc6;
USEVARIABLES ARE gender byconf1-byconf4 byloc1-byloc4
f1conf1-f1conf4 f1loc1-f1loc4
f2conf1-f2conf4 f2loc1-f2loc4;
CATEGORICAL ARE byconf1-byconf4 byloc1-byloc4
f1conf1-f1conf4 f1loc1-f1loc4
f2conf1-f2conf4 f2loc1-f2loc4;
WEIGHT IS weight;
MISSING ARE race (99) gender (99) byconf1-f2loc6 (99);
GROUPING IS gender (0=Male 1=Female);
ANALYSIS: ESTIMATOR=WLSMV;
OUTPUT: SAMPSTAT STANDARDIZED MODINDICES;
MODEL:
f1 BY byconf1@1;
f1 BY byconf2 (2);
f1 BY byconf3 (3);
f1 BY byconf4 (4);
f2 BY byloc1 (5);
f2 BY byloc2 (6);
f2 BY byloc3 (7);
f2 BY byloc4 (8);
f3 BY f1conf1@1;
f3 BY f1conf2 (2);
f3 BY f1conf3 (3);
f3 BY f1conf4 (4);
f4 BY f1loc1 (5);
f4 BY f1loc2 (6);
f4 BY f1loc3 (7);
f4 BY f1loc4 (8);
f5 BY f2conf1@1;
f5 BY f2conf2 (2);
f5 BY f2conf3 (3);
f5 BY f2conf4 (4);
f6 BY f2loc1 (5);
f6 BY f2loc2 (6);
f6 BY f2loc3 (7);
f6 BY f2loc4 (8);
[byconf1$1 f1conf1$1 f2conf1$1] (t1); ! constraining thresholds over time
! thresholds across groups are held equal by default
[byconf1$2 f1conf1$2 f2conf1$2] (t2);
[byconf1$3 f1conf1$3 f2conf1$3] (t3);
[byconf2$1 f1conf2$1 f2conf2$1] (t4);
[byconf2$2 f1conf2$2 f2conf2$2] (t5);
[byconf2$3 f1conf2$3 f2conf2$3] (t6);
[byconf3$1 f1conf3$1 f2conf3$1] (t7);
[byconf3$2 f1conf3$2 f2conf3$2] (t8);
[byconf3$3 f1conf3$3 f2conf3$3] (t9);
[byconf4$1 f1conf4$1 f2conf4$1] (t10);
[byconf4$2 f1conf4$2 f2conf4$2] (t11);
[byconf4$3 f1conf4$3 f2conf4$3] (t12);
[byloc1$1 f1loc1$1 f2loc1$1] (t13);
[byloc1$2 f1loc1$2 f2loc1$2] (t14);
[byloc1$3 f1loc1$3 f2loc1$3] (t15);
[byloc2$1 f1loc2$1 f2loc2$1] (t16);
[byloc2$2 f1loc2$2 f2loc2$2] (t17);
[byloc2$3 f1loc2$3 f2loc2$3] (t18);
[byloc3$1 f1loc3$1 f2loc3$1] (t19);
[byloc3$2 f1loc3$2 f2loc3$2] (t20);
[byloc3$3 f1loc3$3 f2loc3$3] (t21);
[byloc4$1 f1loc4$1 f2loc4$1] (t22);
[byloc4$2 f1loc4$2 f2loc4$2] (t23);
[byloc4$3 f1loc4$3 f2loc4$3] (t24);8.2.4.3 piecewise latent growth model with measurement invariance over time
TITLE: PIECEWISE LATENT GROWTH MODEL WITH MEASUREMENT INVARIANCE OVER TIME
DATA: FILE IS "data\NELSSelfConcept3waves.dat";
FORMAT IS F7 F4 2F2 F11.4 39F2;
VARIABLE: NAMES ARE id status race gender weight
byconf1 byconf2 byconf3 byconf4 byconf5 byconf6 byconf7
byloc1 byloc2 byloc3 byloc4 byloc5 byloc6
f1conf1 f1conf2 f1conf3 f1conf4 f1conf5 f1conf6 f1conf7
f1loc1 f1loc2 f1loc3 f1loc4 f1loc5 f1loc6
f2conf1 f2conf2 f2conf3 f2conf4 f2conf5 f2conf6 f2conf7
f2loc1 f2loc2 f2loc3 f2loc4 f2loc5 f2loc6;
USEVARIABLES ARE byconf1-byconf4 byloc1-byloc4
f1conf1-f1conf4 f1loc1-f1loc4
f2conf1-f2conf4 f2loc1-f2loc4;
CATEGORICAL ARE byconf1-byconf4 byloc1-byloc4
f1conf1-f1conf4 f1loc1-f1loc4
f2conf1-f2conf4 f2loc1-f2loc4;
WEIGHT IS weight;
MISSING ARE race (99) gender (99) byconf1-f2loc6 (99);
ANALYSIS: ESTIMATOR=WLSMV;
OUTPUT: SAMPSTAT STANDARDIZED MODINDICES;
PLOT: TYPE = PLOT3;
SERIES = f1 f3 f5 (*) | f2 f4 f6(*);
MODEL: f1 BY byconf1@1;
f1 BY byconf2 (2);
f1 BY byconf3 (3);
f1 BY byconf4 (4);
f2 BY byloc1 (5);
f2 BY byloc2 (6);
f2 BY byloc3 (7);
f2 BY byloc4 (8);
f3 BY f1conf1@1;
f3 BY f1conf2 (2);
f3 BY f1conf3 (3);
f3 BY f1conf4 (4);
f4 BY f1loc1 (5);
f4 BY f1loc2 (6);
f4 BY f1loc3 (7);
f4 BY f1loc4 (8);
f5 BY f2conf1@1;
f5 BY f2conf2 (2);
f5 BY f2conf3 (3);
f5 BY f2conf4 (4);
f6 BY f2loc1 (5);
f6 BY f2loc2 (6);
f6 BY f2loc3 (7);
f6 BY f2loc4 (8);
[byconf1$1 f1conf1$1 f2conf1$1] (t1);
[byconf1$2 f1conf1$2 f2conf1$2] (t2);
[byconf1$3 f1conf1$3 f2conf1$3] (t3);
[byconf2$1 f1conf2$1 f2conf2$1] (t4);
[byconf2$2 f1conf2$2 f2conf2$2] (t5);
[byconf2$3 f1conf2$3 f2conf2$3] (t6);
[byconf3$1 f1conf3$1 f2conf3$1] (t7);
[byconf3$2 f1conf3$2 f2conf3$2] (t8);
[byconf3$3 f1conf3$3 f2conf3$3] (t9);
[byconf4$1 f1conf4$1 f2conf4$1] (t10);
[byconf4$2 f1conf4$2 f2conf4$2] (t11);
[byconf4$3 f1conf4$3 f2conf4$3] (t12);
[byloc1$1 f1loc1$1 f2loc1$1] (t13);
[byloc1$2 f1loc1$2 f2loc1$2] (t14);
[byloc1$3 f1loc1$3 f2loc1$3] (t15);
[byloc2$1 f1loc2$1 f2loc2$1] (t16);
[byloc2$2 f1loc2$2 f2loc2$2] (t17);
[byloc2$3 f1loc2$3 f2loc2$3] (t18);
[byloc3$1 f1loc3$1 f2loc3$1] (t19);
[byloc3$2 f1loc3$2 f2loc3$2] (t20);
[byloc3$3 f1loc3$3 f2loc3$3] (t21);
[byloc4$1 f1loc4$1 f2loc4$1] (t22);
[byloc4$2 f1loc4$2 f2loc4$2] (t23);
[byloc4$3 f1loc4$3 f2loc4$3] (t24);
i s1 | f1@0 f3@1 f5@1;
i s2 | f1@0 f3@0 f5@1;
ii ss1 | f2@0 f4@1 f6@1;
ii ss2 | f2@0 f4@0 f6@1;
f1-f6@0; ! residual variance fixed at 0;
! f1=i; f2=ii;
! f3=i+s1; f4=ii+ss1;
! f5=i+s1+s2; f6=ii+ss1+ss2;