Chapter 6 Binary Logistic Regression

library(rio); library(ggplot2); library(QuantPsyc); library(psych); library(car); library(reshape)

Binary logistic regression is a form of regression which is used when the DV is a dichotomy and the IVs are of any type. It belongs to generalized linear models.

• For a binary DV, we have two possible outcomes. Let’s take a look at the UCBAdmissions dataset built into R.

# View(UCBAdmissions)
class(UCBAdmissions) # the dataset is a table

## [1] "table"

dat <- as.data.frame(UCBAdmissions) # convert the table to a data frame
class(dat)

## [1] "data.frame"

dat <- reshape::untable(df = dat[, !names(dat) %in% c("Freq")], num=dat$Freq)
# View(dat)

Let’s answer the question: Is there a relationship between gender and admission? Alternatively, do males have a higher chance of being admitted than females? For now, let’s also recode the variables Admit and Gender to be numeric variables with “0”s and “1”s. For the Admit variable, Admitted = 1, Rejected = 0. For the Gender varable, 1 = Female, 0 = Male.

contingency_table1 <- table(dat$Gender, dat$Admit) # contingency table. row is Gender; column is Admit
addmargins(contingency_table1)
prop.table(contingency_table1) # cell percentages
prop.table(contingency_table1, 1) # row percentages
prop.table(contingency_table1, 2) # column percentages

##         
##          Admitted Rejected  Sum
##   Male       1198     1493 2691
##   Female      557     1278 1835
##   Sum        1755     2771 4526
##         
##           Admitted  Rejected
##   Male   0.2646929 0.3298719
##   Female 0.1230667 0.2823685
##         
##           Admitted  Rejected
##   Male   0.4451877 0.5548123
##   Female 0.3035422 0.6964578
##         
##           Admitted  Rejected
##   Male   0.6826211 0.5387947
##   Female 0.3173789 0.4612053

dat$Admit <- ifelse(dat$Admit=="Admitted", 1, 0)
dat$Gender <- ifelse(dat$Gender=="Female", 1, 0)
contingency_table2 <- table(dat$Gender, dat$Admit) # contingency table. row is Gender; column is Admit
addmargins(contingency_table2)
ggplot(dat, aes(x=Gender, y=Admit, color = Gender)) + 
  geom_jitter(width=0, height=0.1) +
  geom_smooth(method = "lm") +
  theme(legend.position = "none")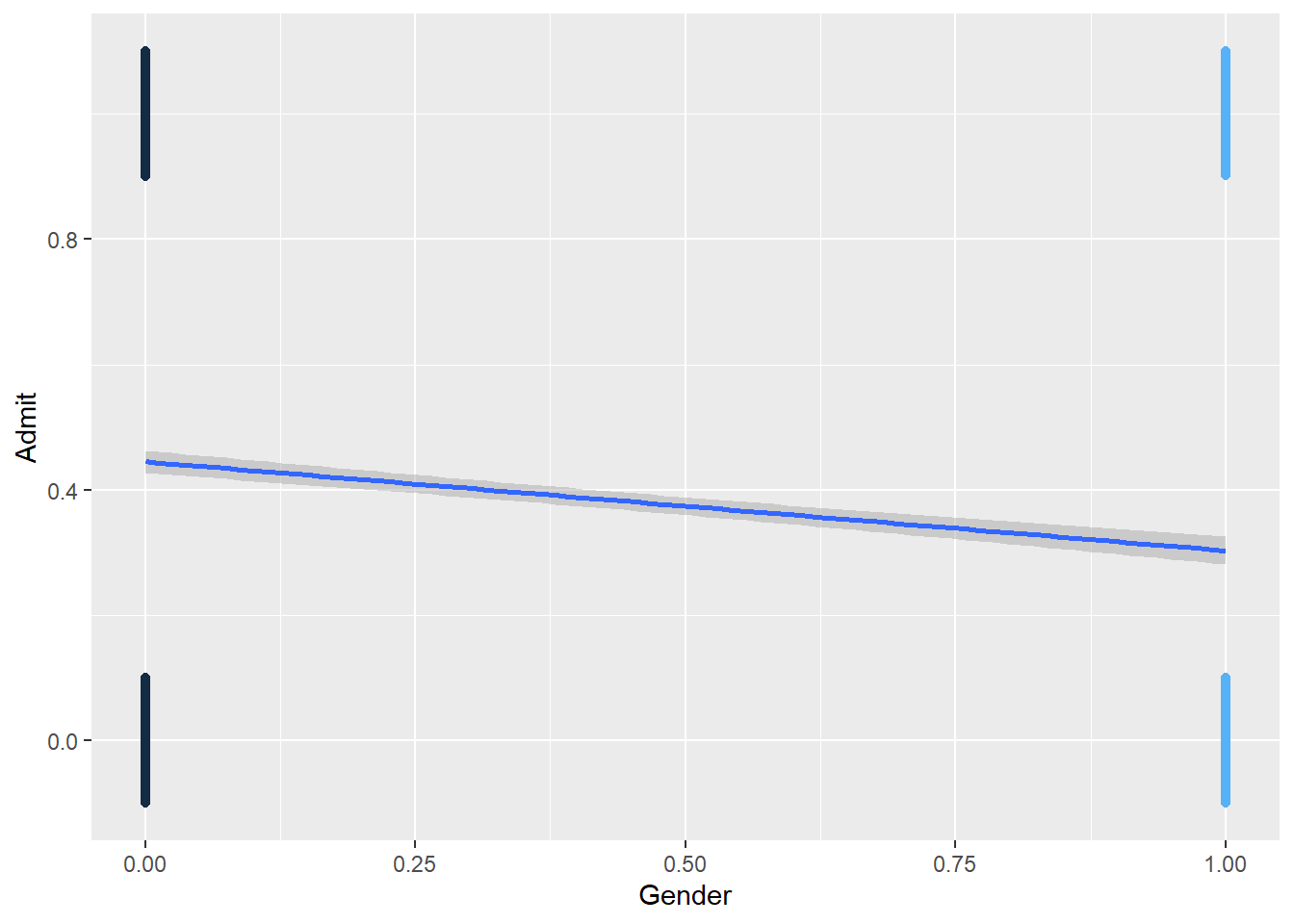

##      
##          0    1  Sum
##   0   1493 1198 2691
##   1   1278  557 1835
##   Sum 2771 1755 4526

6.1 Some Definitions

• Probability of an Event

• Event = Being admitted to college

• Probability of the event P(Admitted) = 0.6

• Odds of an Event

  • Odds is the relative chance of an event
  • Odds of being admitted = $\frac{P\left(Admitted\right)}{1-P\left(Admitted\right)}=\frac{.6}{.4}=1.5$

• If you know the probability of an event, you can get the odds and vice versa.

• Logit = Log-Ods of an Event

  • Logit is the logarithm of the odds. Logit = log(odds)
  • Odds of being admitted = $\frac{P\left(Admitted\right)}{1-P\left(Admitted\right)}=\frac{.6}{.4}=1.5$
  • Logit of being admitted = ${\log }_e\left(Odds\right(Admitted\left)\right)={\log }_e\left(1.5\right)=.405$

• If you know the one of the three: probability, odds, and logit, you can get the values for the other two.

6.2 Logarithm Rules

$${\log }_b\left(XY\right)={\log }_b\left(X\right)+{\log }_b\left(Y\right)$$ $${\log }_b\left(\frac{X}{Y}\right)={\log }_b\left(X\right)-{\log }_b\left(Y\right)$$ $${\log }_b\left(X^k\right)=k{\log }_b\left(X\right)$$ $${\log }_b\left(1\right)=0$$ $${\log }_b\left(b\right)=1$$

$${\log }_b\left(b^k\right)=k$$ $$b^{{\log }_b\left(k\right)}=k$$

Given ${\log }_e\left(A\right)=1.5$, what is A?

$A=e^{{\log }_e\left(A\right)}=e^{1.5}=(2.718282{)}^{1.5}$ where $e$ is a mathematical constant often called Euler’s (pronounced “Oiler”) number.

exp(1.5)

## [1] 4.481689

Given logit = 3, what is the odds?

logit = ${\log }_e\left(Odds\right)=3$

$Odds=e^3$

exp(3)

## [1] 20.08554

6.3 Logistic Regression Equation

Regular OLS Regression $$Y=a+bX+e$$ $$\hat{Y}=a+bX$$

Logistic Regression $$logit=a+bX$$ $$Odds=e^{(a+bX)}$$ $$P(Y=1)=\frac{e^{a+bX}}{1+e^{a+bX}}=\frac{1}{1+e^{-(a+bX)}}$$

6.4 Run Logistic Regression

model <- glm(Admit ~ Gender, family = binomial, data = dat)
summary(model)

## 
## Call:
## glm(formula = Admit ~ Gender, family = binomial, data = dat)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.0855  -1.0855  -0.8506   1.2722   1.5442  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -0.22013    0.03879  -5.675 1.38e-08 ***
## Gender      -0.61035    0.06389  -9.553  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 6044.3  on 4525  degrees of freedom
## Residual deviance: 5950.9  on 4524  degrees of freedom
## AIC: 5954.9
## 
## Number of Fisher Scoring iterations: 4

dat$prob <- fitted(model)
head(dat)

##     Admit Gender Dept      prob
## 1       1      0    A 0.4451877
## 1.1     1      0    A 0.4451877
## 1.2     1      0    A 0.4451877
## 1.3     1      0    A 0.4451877
## 1.4     1      0    A 0.4451877
## 1.5     1      0    A 0.4451877

6.5 Logistic Regression Coefficients

${\log }_e\left(\frac{P\left(Admitted\right)}{1-P\left(Admitted\right)}\right)=-0.22-0.61\ast Gender$

• The outcome is the logit!
• Which group (male vs. female) has a higher logit value?
• How to interprete?
  • “The logit of the female group is 0.61 lower than the logit of the male group.”
• What does this mean?

$-0.61=logit\left(Female\right)-logit\left(Male\right)$

$={\log }_e\left[Odds\right(Female\left)\right]-{\log }_e\left[Odds\right(Male\left)\right]$

$={\log }_e\left[\frac{Odds\left(Female\right)}{Odds\left(Male\right)}\right]$

Therefore, $\frac{Odds\left(Female\right)}{Odds\left(Male\right)}=\exp (-0.61)=0.54$

This is called Odds Ratio. Odds Ratio is the ratio of odds of a comparison/treatment group to that of the reference/control group.

Note: For the UCBAdmissions data, if you conduct a binary logistic regression model for each department separately, you may reach different conclusions regarding gender differences in college admissions. Google .blue[Simpson’s paradox] to learn more.

6.6 Similarities and Differences Between Binary Logistic Regression and OLS Regression

Similarities

• IVs can be continuous, categorical, or a combination of continuous and categorical variables.
• Many of the essential concepts in OLS regression still apply to logistic regression.
  • Model comparison and selection
  • Assumptions (Independence of Errors, Linearity, Multicollinearity; but NOT Normality)
  • Diagnostics (Leverage, Discrepancy, Influence)

Differences

• DV is categorical in logistic regression
• The DV in logistic regression follows a Binomial distribution for which you can specify a link function (logit and probit are two commonly used link functions)
• The estimation method for logistic regression is maximum likelihood, rather than OLS.

6.7 Empirical Example

The Framingham Heart Study

• DV : Coronary Heart Disease (TenYearCHD, yes=1; no=0) status was collected 10 years after the first exam.

• IVs were collected in the first data collection

  • Demographic factors
    • male(male = 1, female = 0)
    • age (in years)
    • education (Some high school=1, high school/GED=2; some college/vocational school=3; college=4)
  • Behavioral risk factors
    • currentSmoker (smoker=1, non smoker=0)
    • cigsPerDay
  • Medical history risk factors
    • BPmeds (On blood pressure medication at time of first exam)
    • prevalentStroker (Previously had a stroke)
    • prevalentHyp (Current hypertension/high blood pressure)
    • diabetes (currently has diabetes)
  • Risk factors from first examination
    • totChol (Total cholesterol, mg/dL)
    • sysBP (Systolic blood pressure)
    • diaBP (Diastolic blood pressure)
    • BMI (Body Mass Index, weight (kg)/height (m^2))
    • heartRate (Heart rate, beats/minute)
    • glucose (Blood glucose level, mg/dL)

dat <- import("data/framingham.csv")
model <- glm(TenYearCHD ~ age, family = binomial, data = dat)
summary(model)

## 
## Call:
## glm(formula = TenYearCHD ~ age, family = binomial, data = dat)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.0386  -0.6261  -0.4580  -0.3695   2.4493  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -5.561090   0.283746  -19.60   <2e-16 ***
## age          0.074650   0.005265   14.18   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 3612.2  on 4239  degrees of freedom
## Residual deviance: 3396.6  on 4238  degrees of freedom
## AIC: 3400.6
## 
## Number of Fisher Scoring iterations: 5

Regression Coefficient

Odds Ratios and Confidence Intervals

exp(model$coefficients)

## (Intercept)         age 
## 0.003844584 1.077507075

exp(confint(model))

##                   2.5 %      97.5 %
## (Intercept) 0.002190705 0.006664767
## age         1.066517962 1.088765650

• One year increase in age is related to 0.075 increase in the logit of having CHD
• Given logit = 0.075, we obtain exp(0.055) = 1.08
• One year increase in age changes the odds of CHD from 1 to 1.08

To Obtain Probabilities

dat$prob <- fitted(model) #<<
df_low_prob <- dat[dat$age < 40, ]
df_mid_prob <- dat[dat$age >45 & dat$age <55, ]
df_high_prob <- dat[dat$age >65,]
ggplot(dat, aes(x=age, y=prob)) +
  geom_point() +
  geom_smooth(data = df_low_prob, method = "lm", se = FALSE, color = "red") + 
  geom_smooth(data = df_mid_prob, method = "lm", se = FALSE, color = "red") +
  geom_smooth(data = df_high_prob, method = "lm", se = FALSE, color = "red")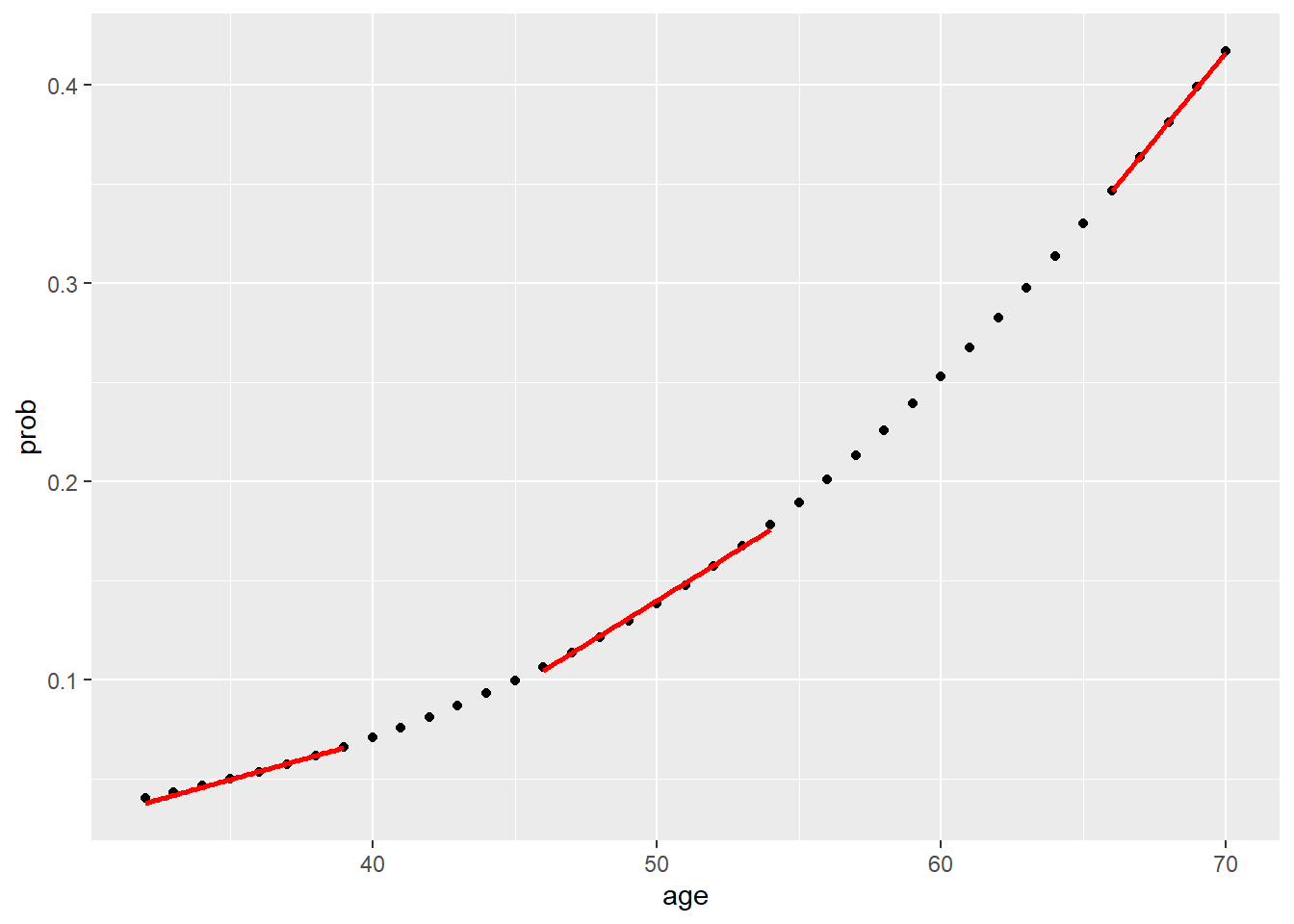

The relationship between age and CHD is positive but not linear.

6.7.1 Assess the model - model chi-square

How much better does the model predict the outcome variable, compared to a baseline model?

• log-likelihood of the model. Analogous to the residual sum of squares in OLS regression
• deviance = -2 X log-likelihood. It has a chi-square distribution.
• model chi-square statistic. Difference between the deviance of the baseline model and the deviance of the current model.

# summary(model)
model.chisq <- model$null.deviance - model$deviance
chisq.df <- model$df.null - model$df.residual
(chisq.prob <- 1 - pchisq(model.chisq, chisq.df)) # right tailed

## [1] 0

6.7.2 Assess the model - $R^2$

logisticPseudoR2s <- function(LogModel) {
  dev <- LogModel$deviance
  nullDev <- LogModel$null.deviance
  modelN <- length(LogModel$fitted.values)
  R.1 <- 1-dev/nullDev
  R.cs <- 1-exp(-(nullDev-dev)/modelN)
  R.n <- R.cs/(1-(exp(-(nullDev/modelN))))
  cat("PseudoR^2 for logistic regression\n")
  cat("Hosmer & Lemeshow R^2: ", round(R.1, 3), "\n")
  cat("Cox & Snell R^2: ", round(R.cs, 3), "\n")
  cat("Naelkerke R^2: ", round(R.n, 3), "\n")
}
logisticPseudoR2s(model)

## PseudoR^2 for logistic regression
## Hosmer & Lemeshow R^2:  0.06 
## Cox & Snell R^2:  0.05 
## Naelkerke R^2:  0.086

6.7.3 Diagnostics

dat$leverage <- hatvalues(model) # leverage
dat$studentized.residuals <- rstudent(model) # discrepancy
dat$cooks.d <- cooks.distance(model)  # influence
dat$leverage[(dat$leverage > 3 * mean(dat$leverage))] 

##   [1] 0.001661901 0.001459850 0.001459850 0.001661901 0.001459850 0.001459850 0.001661901 0.001661901 0.001459850 0.001661901 0.001880347
##  [12] 0.001661901 0.001661901 0.001880347 0.001459850 0.001459850 0.001661901 0.001459850 0.001661901 0.001661901 0.001661901 0.001459850
##  [23] 0.001880347 0.001459850 0.001459850 0.001459850 0.001661901 0.001661901 0.001661901 0.001459850 0.001661901 0.001661901 0.001880347
##  [34] 0.001661901 0.001459850 0.001459850 0.001880347 0.001459850 0.001459850 0.001661901 0.001661901 0.001661901 0.001661901 0.001661901
##  [45] 0.001459850 0.002362781 0.001459850 0.001459850 0.001661901 0.001459850 0.001459850 0.001661901 0.001459850 0.001661901 0.001880347
##  [56] 0.001459850 0.001661901 0.001459850 0.001459850 0.001459850 0.001459850 0.001459850 0.001661901 0.001661901 0.001880347 0.001661901
##  [67] 0.001661901 0.001459850 0.001880347 0.001661901 0.001880347 0.001661901 0.001661901 0.001880347 0.001661901 0.001661901 0.001661901
##  [78] 0.001880347 0.001459850 0.002114350 0.001661901 0.002362781 0.001661901 0.001459850 0.002114350 0.002114350 0.001459850 0.001459850
##  [89] 0.001880347 0.001459850 0.001661901 0.001880347 0.001661901 0.001459850 0.001880347 0.002114350 0.001661901 0.001661901 0.001880347
## [100] 0.001880347 0.001661901 0.001880347 0.001661901 0.001459850 0.001459850 0.002114350 0.002114350 0.001661901 0.002114350 0.001880347

dat$studentized.residuals[abs(dat$studentized.residuals) >3]

## numeric(0)

dat$cooks.d[dat$cooks.d>1]

## numeric(0)

dat$studentized.residuals[(abs(dat$studentized.residuals) > 3)]

## numeric(0)

outlierTest(model)

## No Studentized residuals with Bonferroni p < 0.05
## Largest |rstudent|:
##     rstudent unadjusted p-value Bonferroni p
## 782 2.451316           0.014234           NA

dat$cooks.d[dat$cooks.d >1]

## numeric(0)

6.7.4 Assumptions - Linearity

dat$log.age.Int <- log(dat$age)*dat$age #<<
model.linearity <- glm(TenYearCHD ~ age + dat$log.age.Int, data = dat, family = binomial()) #<<
summary(model.linearity)

## 
## Call:
## glm(formula = TenYearCHD ~ age + dat$log.age.Int, family = binomial(), 
##     data = dat)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -0.9096  -0.6538  -0.4639  -0.3403   2.5935  
## 
## Coefficients:
##                  Estimate Std. Error z value Pr(>|z|)    
## (Intercept)     -13.45767    3.46917  -3.879 0.000105 ***
## age               0.83681    0.33290   2.514 0.011947 *  
## dat$log.age.Int  -0.15396    0.06721  -2.291 0.021975 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 3612.2  on 4239  degrees of freedom
## Residual deviance: 3391.2  on 4237  degrees of freedom
## AIC: 3397.2
## 
## Number of Fisher Scoring iterations: 5

6.7.5 Assumptions - Independence of errors

dwt(model)

##  lag Autocorrelation D-W Statistic p-value
##    1      0.02687873      1.946162   0.074
##  Alternative hypothesis: rho != 0

6.7.6 Use more predictors

dat$edu.c <- factor(dat$education)
levels(dat$edu.c) <- c("some high school", "high school/GED", "some college/vocational", "college")
model2 <- glm(TenYearCHD ~ age + male + sysBP + edu.c, family = binomial, data = dat)
summary(model2)

## 
## Call:
## glm(formula = TenYearCHD ~ age + male + sysBP + edu.c, family = binomial, 
##     data = dat)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.5951  -0.5995  -0.4423  -0.3124   2.8506  
## 
## Coefficients:
##                               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)                  -7.427112   0.379871 -19.552  < 2e-16 ***
## age                           0.058923   0.005893   9.999  < 2e-16 ***
## male                          0.612284   0.093217   6.568 5.09e-11 ***
## sysBP                         0.017947   0.002002   8.967  < 2e-16 ***
## edu.chigh school/GED         -0.179544   0.114138  -1.573    0.116    
## edu.csome college/vocational -0.100398   0.136901  -0.733    0.463    
## edu.ccollege                 -0.007083   0.151157  -0.047    0.963    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 3522.6  on 4134  degrees of freedom
## Residual deviance: 3186.8  on 4128  degrees of freedom
##   (105 observations deleted due to missingness)
## AIC: 3200.8
## 
## Number of Fisher Scoring iterations: 5

6.7.7 Check Multicollinearity Among IVs

vif(model2)

##           GVIF Df GVIF^(1/(2*Df))
## age   1.167782  1        1.080640
## male  1.054028  1        1.026659
## sysBP 1.144721  1        1.069916
## edu.c 1.077856  3        1.012574

6.7.8 Interprete results

Regression Coefficients

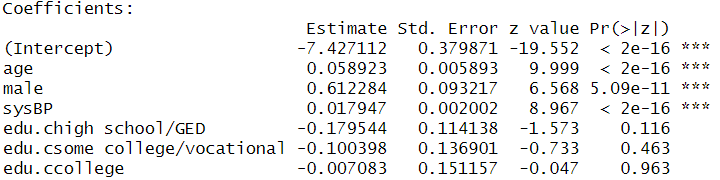
Odds Ratios and Confidence Intervals

exp(model2$coefficients)

##                  (Intercept)                          age                         male                        sysBP 
##                 0.0005949034                 1.0606932534                 1.8446390825                 1.0181093723 
##         edu.chigh school/GED edu.csome college/vocational                 edu.ccollege 
##                 0.8356510686                 0.9044777525                 0.9929417559

exp(confint(model2))

##                                     2.5 %      97.5 %
## (Intercept)                  0.0002801087 0.001242352
## age                          1.0485587804 1.073069542
## male                         1.5372823946 2.215676632
## sysBP                        1.0141309942 1.022122846
## edu.chigh school/GED         0.6670598320 1.043750212
## edu.csome college/vocational 0.6888360992 1.178746245
## edu.ccollege                 0.7343253293 1.329077617

• Coefficient for “male.”
  • A male is more likely to have CHD than a female adjusting for the effects of other variables.
  • The odds of having CHD for a male is predicted to be 1.85 ( $e^{0.612}$) times the odds of of having CHD for a female, holding the other variables constant.
• Coefficient for “age.”
  • The older the person grew, the more likely the person would have CHD.
  • The odds of having CHD is predicted to increase by a factor of 1.06 ( $e^{0.0589}$) with one year increase in age, holding the other variables constant.
• Coefficients for the coded dummy variables for education.
  • None of them was statistically significant. Education level was not statistically significantly associated with the odds of having CHD, holding the other variables constant.
  • If they were statistically significant, a person who finished high school is less likely to have CHD than a person who only had some high school eduation, holding the other variables constant. The odds of having CHD for a person who finished high school is predicted to decrease by a factor of 0.835( $e^{-.180}$) than a person who only had some high school education, holding the other variables constant.
  • The coefficients for the dummy variables compare one group’s odds of having CHD with the odds of the reference group (i.e., those with some high school education).